地下水是重要的飲用水源. 由于人類發展忽略了環境保護,導致地下水污染嚴重,其中硝酸鹽污染問題突出[1]. 過量的硝酸鹽會對人類健康造成嚴重危害,例如藍嬰病[2]. 因此,治理地下水硝酸鹽刻不容緩[3].
目前,國際上地下水硝酸鹽污染治理技術分為原位處理技術和抽出處理技術. 抽出處理技術仍然是最常用的一種. 抽出處理技術的核心在于如何有效地把污染的地下水從含水層中抽出來,通常考慮的因素包括抽水井的位置、 抽水井數、 抽水速率、 安裝井和抽水處理成本,需要找到一個合適的方法得到最優解,從而使治理成本最小化[4]. 因此,其關鍵是多目標優化問題. 目前,國外已有許多模擬優化技術運用到抽出處理技術設計[5]. 傳統的優化方法包括線性規劃、 非線性規劃、 動態規劃、 二次規劃和整數規劃[6]. 較新的優化方法包括遺傳算法(GA)[7, 8, 9, 10, 11]和模擬退火法(SA)[12, 13, 14, 15, 16]. 這些優化方法可以耦合到地下水模擬模型中.
抽出處理在優化過程中容易陷入局部優化. GA和SA采用了多種全局優化方法,能夠實現全局優化. Dougherty等[17]首次將模擬退火法(SA)運用到地下水修復最優設計,在其設計中包含井的安裝費用和抽水費用. McKinney等[18]運用遺傳算法解決了最大抽水量和最低抽水成本等地下水優化問題. Yoon等[19]運用實數編碼遺傳算法來確定最優抽水速率和最佳井的位置,最大限度減小了地下水修復系統成本. Erickson等[20]利用小生境技術遺傳算法解決了抽出處理地下水修復問題,實現了修復成本和剩余污染物濃度最小化. 吳劍鋒等[21]開發改進了一種小生境Pareto遺傳算法(INPGA),以美國麻省軍事保護區為實例,通過建立研究區復雜地下水污染治理的多目標優化管理模型,并添加消息傳遞接口(MPI)的并行計算和個體適應度,提高了運行庫計算速度.
本文以北京某場地生活垃圾填埋場硝酸鹽污染地下水為研究對象,采用Visual MODFLOW 4.6中Modular Groundwater Optimizer (MGO)[22],將水流模擬軟件 MODFLOW、 溶質運移MT3DMS與遺傳算法和模擬退火法相結合,嘗試解決地下水硝酸鹽污染抽出處理優化模擬,優化井的位置、 井的抽水速率及最小化治理成本. 其執行程序通過FORTRAN自動編碼器來匯編,屬于內置模塊,在優化過程中采用DOS界面運行.
1 地下水硝酸鹽抽出處理優化系統設計
1.1 遺傳算法
遺傳算法(Genetic Algorithm)是模擬達爾文生物進化論的自然選擇和遺傳學機理的生物進化過程的計算模型,是一種通過模擬自然進化過程搜索最優解的方法,它最初由美國Michigan大學Holland教授于1975年首先提出. 采用概率化的尋優方法,能自動獲取和指導優化的搜索空間,自適應地調整搜索方向,不需要確定的規則. 遺傳算法的核心是選擇、 交叉、 變異. 更多遺傳算法的描述參見文獻[23, 24]. 從任一初始種群出發,通過選擇、 交叉、 變異操作,產生一群更適應環境的個體,檢查其結果是否符合優化的要求,如果不符合,重復其上述過程,直到優化出滿意的結果.
1.2 模擬退火法
模擬退火法,源于統計熱力物理學,它模擬熔融狀態下物體逐漸冷卻達到結晶狀態的物理過程. 材料中的原子原來會停留在使內能有局部最小值的位置,加熱使能量變大,原子會離開原來位置,而隨機在其他位置中移動. 退火冷卻時速度較慢,使得原子有較多可能可以找到內能比原先更低的位置. 不依賴初始模型的選擇,能尋找全局最小點而不陷入局部極小[19]. 模擬退火算法的操作步驟如下.
步驟1:給定初始溫度T0解X0算f0=f(x0); 步驟2:隨機產生擾動Δx,計算f1=f(x0+Δx)和Δf=f1-f0; 步驟3:若Δf≤0則轉步驟5,否則產生隨機數R∈[0,1]; 步驟4:若p=exp(-Δf/T)≥R,則用x′=x0+Δx代替x0, f1代替f0; 步驟5:檢查M過程是否結束,若未結束則轉步驟2; 步驟6:降低溫度參數T; 步驟7:判斷終止準則是否滿足,若滿足,則算法終止,否則,轉步驟2.
1.3 地下水多目標優化模型
地下水優化模型通常包含兩組變量:決策變量和狀態變量. 在優化過程中的目的是識別這些決策變量的最佳組合. 狀態變量依賴地下水流方程的水頭和地下水溶質運移方程的濃度. MODFLOW水流方程如下:
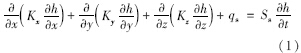
式中,Kx、 Ky、 Kz分別為滲透系數在x、 x、 y方向的分量; h表示水頭(m); qs表示單位時間從單位體積含水層流入或流出的水量(d-1); Ss表示貯水率(m-1); t表示時間(d). MT3DMS地下水溶質運移方程:
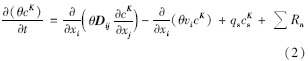
式中,θ表示含水層的孔隙度(無量綱); cK表示溶質組分K的濃度(mg ·L-1); D ij是水動力彌散系數張量(m2 ·d-1); vi是孔隙中實際水流速度(m ·d-1); qs表示單位時間從單位體積含水層流入或流出的水量(d-1); cKs是源匯項溶質組分K的濃度(mg ·L-1); Rn表示化學反應項總和[mg ·(L ·d)-1].
優化設計過程中,目標函數包含井的安裝費用、 抽水費用、 抽水地下水硝酸鹽治理費用等. 其數學表達式如下.
最小化:
約束條件:
式中,J表示目標函數,a1表示安裝一口井的總費用,W表示研究區備選井的數量,N是總的優選井數量,即從備選井中優化出來井的數量,a2是抽出和處理單位體積的水的費用[4],Qi單位時間抽水的體積(m3 ·d-1),Qmin和Qmax分別是最小抽水和最大抽水量,Δti是井i持續抽水時間(d),hi是井i的水頭(m),hmin和hmax分別是最小水頭和最大水頭(m); ci是井i的溶質的濃度(mg ·L-1),c*表示目標治理濃度(mg ·L-1). 上述定義多目標優化方案也可以通過試錯法解決. 雖然試錯法簡單、 易用,但測試和檢驗煩瑣,且不能保證組合的最優方案,容易產生局部優化,往往很難找到最優的抽出處理方案. 所以在滿足所有約束條件下,應用遺傳算法和模擬退火法比試錯法更有效解決井的位置及組合問題[22].
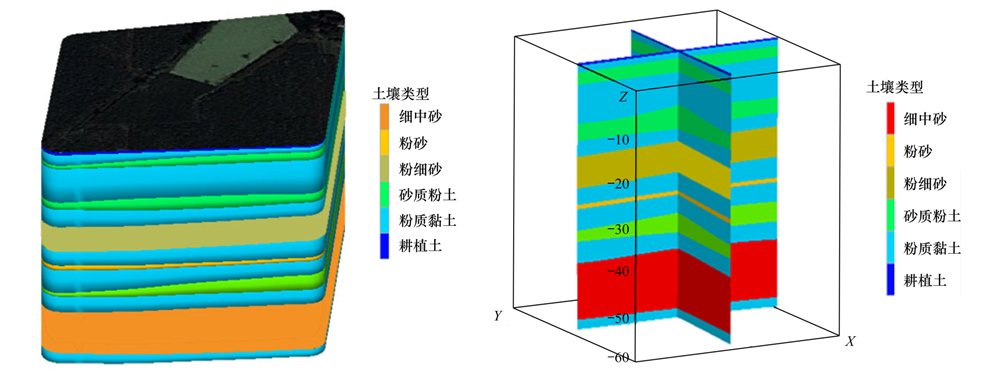
圖 2 研究區三維地質剖面
2 材料與方法
2.1 研究區水文地質條件
研究區位于北京某場地,所處區域地勢平坦. 場地東側為養殖場,西南側為當地農民耕作農田,農村垃圾和畜禽養殖廢水均排放到池塘(圖 1).
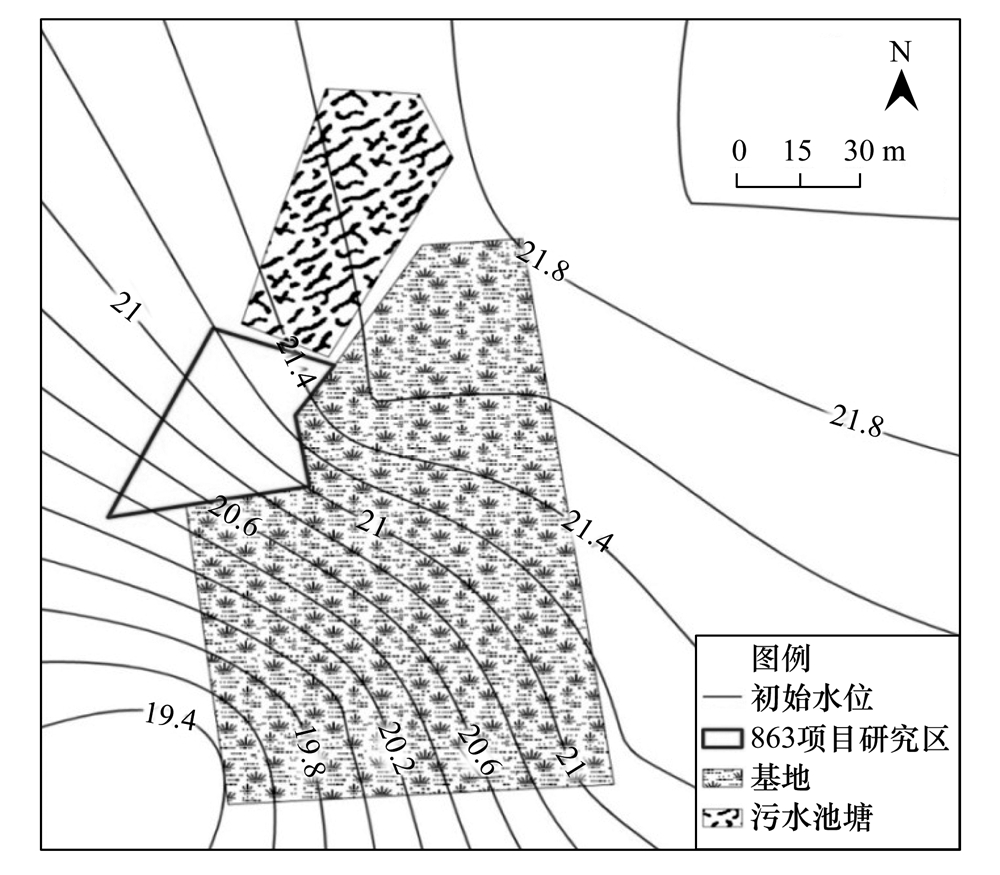
圖 1 研究區初始流場示意
依據場地調查資料,利用CTECH對研究區構建三維地質剖面圖,第一層主要含水層為非承壓含水層,地下水標高16~23 m,厚度約6.92 m,以粉細砂為主,局部夾有砂質粉土、 黏質粉土和粉質黏土(圖 2). 研究區第一含水層下面主要為砂質粉土、 黏質粉土,滲透性很差,能夠起到較好的隔水作用.
在研究區進行單孔抽水試驗. 通過Aquifer Test軟件分析,結果見表 1. 研究區含水層的平均滲透系數為3.37 m ·d-1.
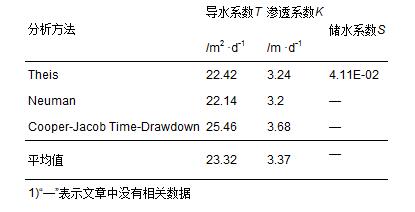
表 1 不同求參方法中滲透系數和導水系數結果表
2.2 研究區地下水污染狀況
利用Geoprobe鉆機對生活垃圾填埋場地下水及池塘污水進行取樣調查. 現場測試數據:池塘地表水的NH+4-N高達46.8 mg ·L-1,同時地表 50 cm滲坑NO-3-N高達65 mg ·L-1. 研究區地下水硝酸鹽仍處于不斷變化的情況,同時場地調查尚不夠充分,不足以刻畫出實際地下水硝酸鹽的污染羽狀況. 因此,本研究以農村垃圾和畜禽養殖廢水為污染源,硝酸鹽入滲濃度為65 mg ·L-1,模擬在天然地下水流動情況下釋放5 a形成的硝酸鹽污染羽作為抽出處理的初始污染羽. 研究區硝酸鹽初始污染羽總量為36.99 kg,見圖 3.
2.3 抽出處理備選井方案
為了設計合理的抽出處理治理優化方案,根據模擬生成硝酸鹽污染羽形成的范圍及通過試錯法確定的較為有效的抽水井位置,在研究區布置了18口備選井方案(圖 3). 目的是在滿足治理成本最小情況下,抽出處理后達到目標治理濃度,同時確定最佳井數及其井的位置和抽水速率.
研究區周圍地下水硝酸鹽背景濃度約為1 mg ·L-1. 將研究區紅色框作為濃度約束區,在100 d抽出處理修復時間內,其硝酸鹽目標修復濃度低于10 mg ·L-1.
2.4 模型概化及參數確定
研究區場地范圍較小,可以將研究區假設為均質各向異性含水層. 地下水硝酸鹽污染濃度主要分布在第一含水層,該層下部主要為砂質粉土、 黏質粉土,滲透系數較差,能夠起到較好的隔水作用,故 而將含水層概化成一層. 研究場地為225 m×200m,將其剖分成2.25 m×2 m. 地下水從北東方向向南西方向流(圖 1). 研究區的初始水力坡度約為0.01. 西北方向和東南方向為隔水邊界. 地下水硝酸鹽的阻滯因子設為1. 地下水流模擬設置為穩定流模擬(兩種優化方法只適合穩定流[4]),模型輸入參數見表 2.
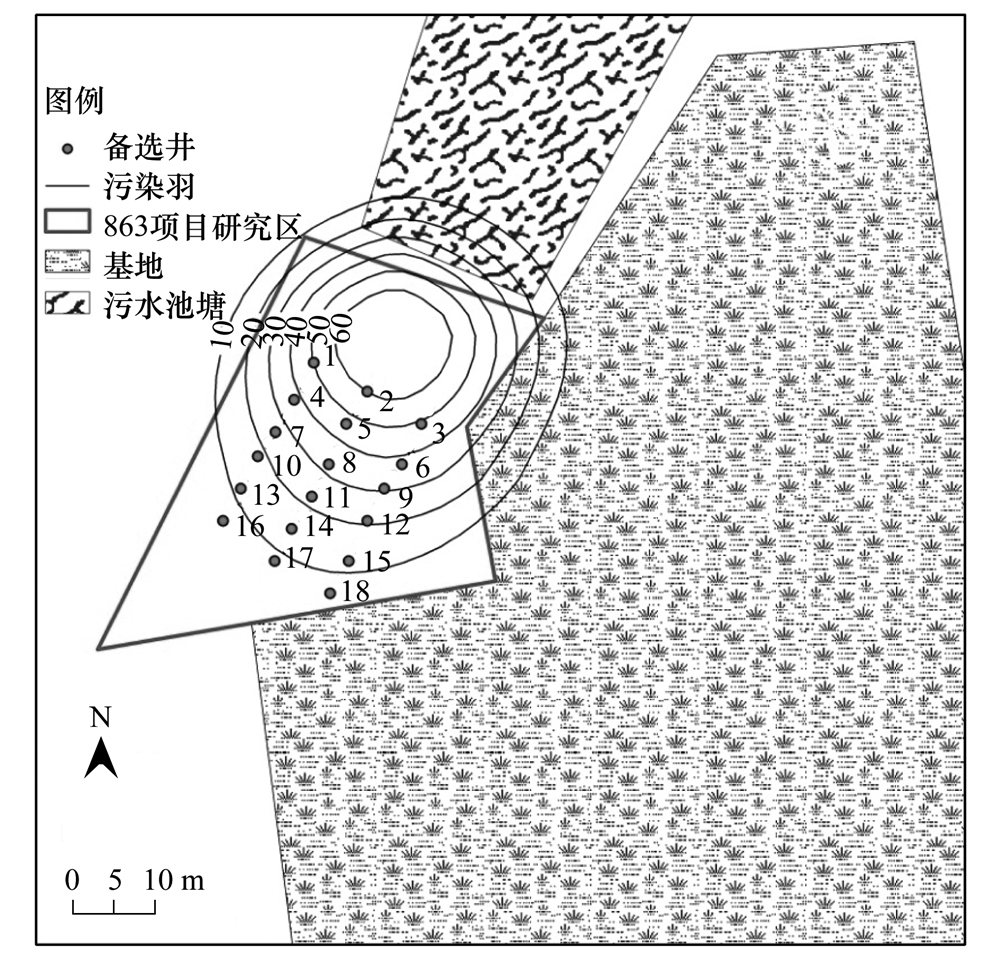
圖 3 地下水硝酸鹽初始污染羽分布示意和備選井位置
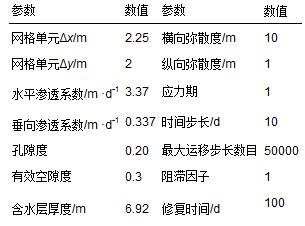
表 2 模型輸入參數
表 3列出了安裝一口井的總費用、 抽出和處理單位體積水的費用[4]. 最小與最大水頭值、 最小與最大抽水量及硝酸鹽目標治理濃度等約束條件.
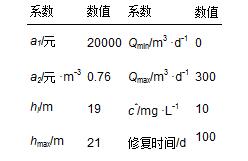
表 3 費用系數和約束變量
3 優化結果分析與討論
3.1 抽出處理優化
本研究中GA設定的相關參數如下:種群數目為100,最大遺傳代數為100,每口井的抽水速率離散化區間數為32,交叉概率為0.90,變異概率為0.05. SA設定的相關參數如下:初始溫度為1,抽樣次數10000,降溫率為0.9,最大迭代次數為100.
兩種優化方法都要求濃度約束區治理100 d后的地下水硝酸鹽(以氮計)達到10 mg ·L-1. GA優化結果:8號井優化抽水速率為155 m3 ·d-1,14號井優化抽水速率為10 m3 ·d-1; SA優化結果:8號井優化抽水速率為82 m3 ·d-1,14號井優化抽水速率為39 m3 ·d-1. 其他井都為零(表 4). GA在8號井優化的抽水速率比SA在8號井的要大,在14號井優化的抽水速率比SA在14號優化的速率要小. 但SA總抽水速率(121 m3 ·d-1)比GA(165 m3 ·d-1)小.
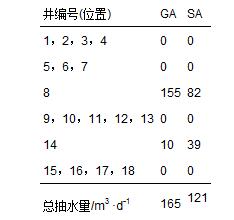
表 4 優化井位置與抽水速率
基于GA和SA優化的抽水速率,100 d后硝酸鹽總去除量分別為28.45 kg和31.42 kg,其總量去除率分別76.89%和84.92%,見圖 4. 優化過程中發現,總抽水速率和硝酸鹽總去除量存在近似線性增加的趨勢.
GA、 SA同時優化了井的位置和抽水量. 圖 4可以看出研究區中18口備選井方案,兩種優化方法最優的兩口井都是8號井和14號井. 說明在該場地抽出處理中,只需要2口井就可以滿足約束條件,到達治理目標,比初始方案減少16口井,節省了井的安裝成本. 同時說明最優井的位置在污染羽的中軸線上中游和中下游抽水布置最為合理.

圖 4 GA和SA抽水治理100 d后地下水硝酸鹽分布示意
3.2 GA與SA對比分析
GA、 SA不僅可以優化井的位置、 抽水速率及井數,而且還可以優化系統治理成本(井安裝成本與抽出處理成本之和),見表 5. GA和SA優化井數一樣,其安裝成本也就一樣,但SA優化總的抽水量比GA要低,所以SA優化的系統成本要比GA要低,說明SA在多目標地下水硝酸鹽修復優化管理要比GA體現出一定的優越性,體現在節省系統治理成本.
圖 5為GA與SA遺傳代數與目標函數優化收斂對比. GA在40代后優化目標函數趨于收斂,而SA在20代后趨于穩定. GA在前20代目標函數優化波動性比SA要大. 兩者最終都趨于穩定. 兩種優化方法識別決策變量的最佳組合. 在最小化治理成本下,全局優化井數、 井的抽水量、 安裝成本、 抽水處理成本,使得優化結果可信. SA的系統治理成本要比GA少3338.45元,節省成本約6.8%,見表 5具體參見污水寶商城資料或http://www.bnynw.com更多相關技術文檔。
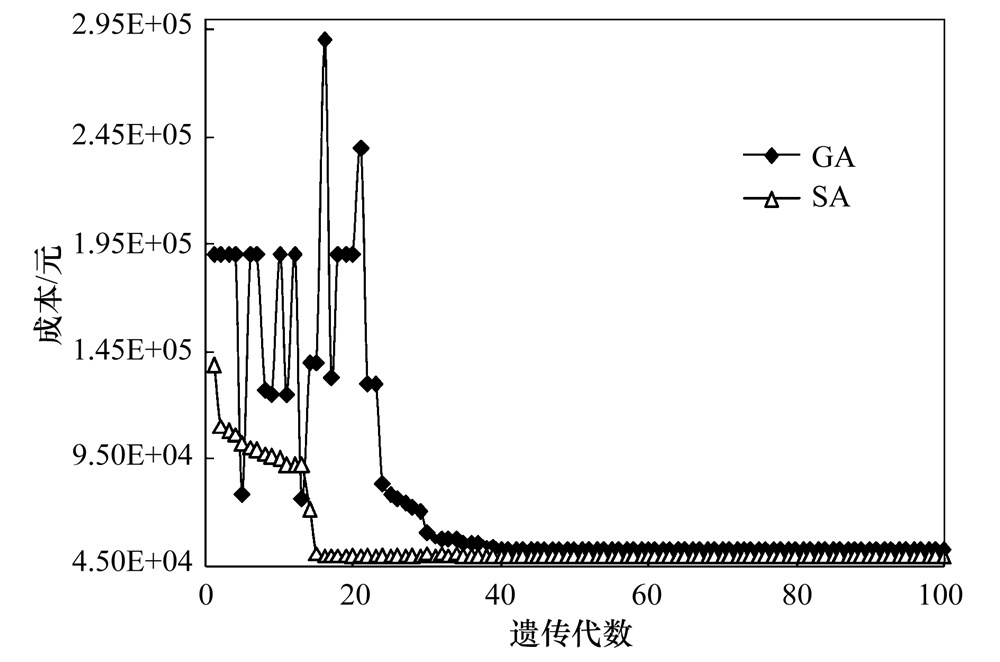
圖 5 GA、 SA目標函數優化收斂對比

表 5 GA、 SA優化系統治理成本/元
4 結論
(1)本研究依據北京某場地調查資料,利用遺傳算法(GA)和模擬退火法(SA)對地下水硝酸鹽污染羽治理區中布置18口備選井方案進行優化. 為達到100 d將研究區硝酸鹽濃度降低到10 mg ·L-1的目標,GA和SA優化的井都為8號井和14號井,優化總抽水速率分別為165 m3 ·d-1和121 m3 ·d-1,同時其硝酸鹽總量去除率分別為76.89%和84.92%.
(2)優化結果說明,最佳井的位置應位于硝酸鹽污染羽中游及中下游的中軸線上,且中游抽水速率比下游要大. 兩種優化算法對比表明模擬退火法(SA)優化系統治理成本比遺傳算法(GA)節省6.8%,且波動性小,更收斂.
(3)模擬退火法(SA)和遺傳算法(GA)耦合到地下水流模擬程序MODFLOW和溶質運移程序MT3DMS中,可以設計合理的抽出處理方案和符合管理目標修復系統,為地下水污染現場修復提供科學的指導.
致謝: 本研究場地基礎信息調查由中國環境科學研究院、 北京建工環境修復有限責任公司、 輕工環保研究所等共同完成. 此外,南京大學吳劍鋒老師對遺傳算法優化方法工作給予指導!在此一并表示感謝.(來源及作者:中國地質大學(北京)水資源與環境學院, 水資源與環境工程北京市重點實驗室 姜烈、何江濤、姜永海、劉菲)


