絮凝過程中絮體生長的研究

中國污水處理工程網時間：2016-7-15 14:00:29

污水處理技術 | 匯聚全球環保力量，降低企業治污成本

　　1 引言

　　絮凝是混凝水處理過程中的重要階段之一.絮凝過程中，絮體粒徑分布及形態學特征時刻變化，其群體形貌動態變化過程復雜.近年來，許多學者采用分形數學理論來描述絮體在不同工況條件下的顆粒幾何特征，以期通過定量描述絮體形貌的復雜性，揭示絮體形成及其與工藝效能的內在關系.

　　眾所周知，凝聚是一個顆粒隨機碰撞的過程，具有非線性特征.分形維數常用來描述具有自相似結構的不規則幾何體的非線性工作機理.在絮凝過程中，絮體顆粒形態和粒徑分布時刻變化，而簡單分形維數主要用于描述和表征顆粒群體的整體性和平均性，不能完全揭示絮體分形變化的動力學過程(張德祥等，2007;Brown et al., 1992).多重分形描述不同局部條件或不同層次所導致的特殊結構行為與特征，從系統的局部出發來研究整體的特征，并借助統計物理學的方法討論特征參量概率測度的分布規律.目前多重分形理論已廣泛應用于土壤環境(Grout et al., 1998;Li et al., 2011)、材料(Pérez et al., 2012)、地球科學(García-Marín et al., 2008)、醫學(Song et al., 2013;Vasiljevic et al., 2012)、城市規劃(Ariza-Villaverde et al., 2013)等諸多領域，在國內外水處理領域中未見相關研究內容.實際檢測操作中對特定絮體的生長過程監測存在困難，但絮體的群體生長在一定范圍內存在統計學自相似特征和標度不變性，可以用多重分形理論研究并定量描述絮體的生長規律.

　　絮體形態和分布特征的定量化對絮凝機理的完善和工藝控制均有重要的理論價值.本研究在前人基礎上采用多重分形理論定量描述絮體群在生長過程中的分布特征，探討絮體在生長過程中的多重分形行為.

　　2 分形及多重分形理論

　　1977年，M and elbrot將分形集的概念引入并對分形的定義進行了闡述.分形維數區別于歐式幾何中對象的拓撲維數，它是描述非線性復雜系統特征的工具.分形幾何學廣泛應用于圖形圖像的分析處理，對于不規則形狀物體的二維數字圖像，應用計算機程序可以非常方便的計算物體的分形維數.計算分形維數的方法有很多，有盒計維數、相似維數、容量維數、關聯維數、信息維數、面積周長維數等.盒計維數是在計算機圖形圖像處理中應用最廣泛的分形維數算法之一，其基本的算法原理是以不同測度的盒子來測量目標數目，最后得到一個形如下式的冪函數關系：

　　式中，N為目標數目，ε為盒子大小.兩邊取對數后得到：

　　式中，D即為分形維數.

　　多重分形是在簡單分形基礎上發展的分形理論，自1980年即已成為不規則物體形態分析的基本工具(Ficker，2004).多重分形譜由兩種關系組成，一種是由一系列概率Pi，ε所組成的子集與測度之間的冪函數關系：Pi，ε∝εα，α稱為奇異指數，其反映的是分形圖像中概率集合隨測度的變化關系，即反映了分形對象的奇異程度;另一種是一系列測度下的盒子數N(ε)與測度之間的冪函數關系：N(ε)∝εf(α).此處f(α)即為多重分形譜，顯然它表示的是同一α值子集的分形維數.

　　多重分形譜的計算處理過程，首先需定義配分函數，此函數是對概率的加權求和，即：

　　式中，加權系數q> >1，則配分函數中大概率子集占主導，q< <-1，則配分函數中小概率子集占主導.通過加權，可將一種分形拓展為多種奇異程度的分形，從而可將分形集的內部結構完整呈現出來(孫霞等，2003).

　　對于二維圖像的多重分析，概率Pi，ε為盒子中研究目標所占的像素數量與圖像中研究目標所占的總像素數量比：

　　配分函數與尺度ε存在冪函數關系Iq(ε)= ετ(q)，兩邊取對數，則可得到

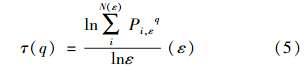
　　此處τ(q)稱為質量指數，其反映的是Iq(ε)與lnε的線性關系，這種關系指定分形的無標度性.

　　廣義分形維數Dq隨q值的不同而具有不同的意義，其定義式如下：

　　當q=0，此時I0反應二維圖像中對象的空間幾何性質，與概率P無關，這樣D0就表示普通的豪斯道夫維數，此時對應于f(α)max(謝淑云等，2009).

　　根據τ(q)和q的關系經統計物理學中的勒讓德變換后得到：

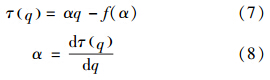
　　由此可得到，α-f(α)的關系，即多重分形圖譜.根據多重分形理論，多重分形譜攜帶大量研究對象的定量信息，f(αmax)、αmax反映的是概率最小子集的性質;f(αmin)、αmin反映的是概率最大子集的性質，f(α)max和其對應的α0反映的是最或然子集的性質;多重分形譜譜寬Δα=αmax-αmin反映了概率分布范圍的大小，概率分布愈不均勻，相應的譜寬會越大;Δf(α)=f(αmax)- f(αmin)反映的是最大、最小概率單元數目之間的比例關系(Ficker，2004).

　　3 試驗材料及方法

　　3.1 試驗材料

　　原水為人工配制高嶺土渾濁液，濁度(100±3)NTU.混凝劑為聚合硫酸鐵(PFS，投加濃度30 mg · L-1).試驗設備為一套混凝圖像在線監測系統，主體反應槽是容積為15 L的有機玻璃制圓形反應罐，IKA在線程序可控攪拌器，Prosical相機(相機設置像素512×512，像素大小7.4 μm ×7.4 μm，最小快門速度20 μs)實時捕捉圖像，理論識別能力50 μm.

　　裝置示意圖如圖 1所示，整個反應過程在反應槽內進行，少量反應懸濁液在蠕動泵的工作下以一定流速通過側向打開的圖像采集通道，圖像采集通道尺寸為3 mm×50 mm×200 mm;打開光源控制器，將相機對焦以看清通道內絮體，相機采集流經通道的懸浮顆粒圖像并將圖像保存在計算機上待軟件分析.

圖 1 混凝圖像在線監測系統示意圖

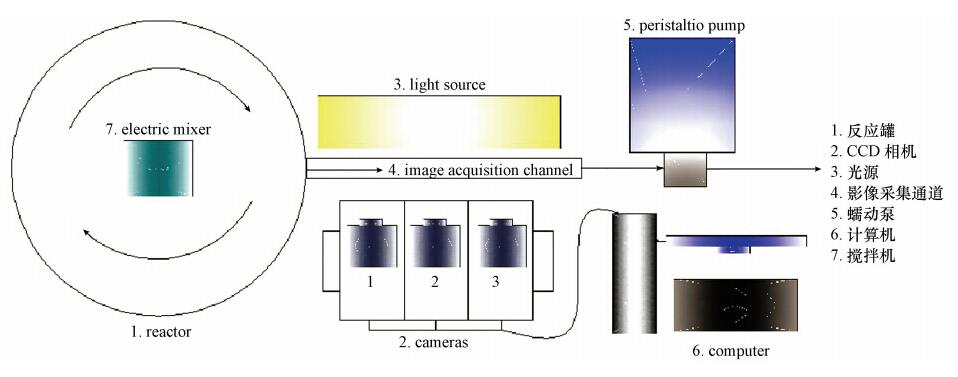
　　3.2 試驗方法

　　反應槽內進行混凝劑聚合硫酸鐵處理模擬地表水試驗，反應共歷時770 s.將配制好的聚合鐵混凝劑投入水中，在轉速200 r · min-1的條件下快速攪拌50 s;然后慢速攪拌720 s，轉速75 r · min-1.懸濁液以10 mm · s-1的流速流經圖像采集通道，相機每10 s采集1次圖像并保存于計算機中，視窗大小2.19 cm×2.19 cm.

　　圖像處理：該文所采用圖像處理軟件為Image-Pro Plus，相機采集到的圖像格式為256灰度圖，通過軟件進行閾值轉換法二值化處理后，計算圖像上的顆粒數目、平均粒徑(等效投影面積直徑)，并計算圖像的多重分形譜.

　　多重分形譜計算程序的參數設置：加權系數q取10，盒子大小取8、12、16、32、64、128、256、512.

　　4 結果及分析(Results and analysis) 4.1 絮體的生長過程

　　混凝劑在快速攪拌條件下迅速分散到水中，此階段混凝劑與水充分混合并水解，使水中懸浮顆粒脫穩，進入慢速攪拌階段，脫穩顆粒開始凝聚，即絮體開始生長.

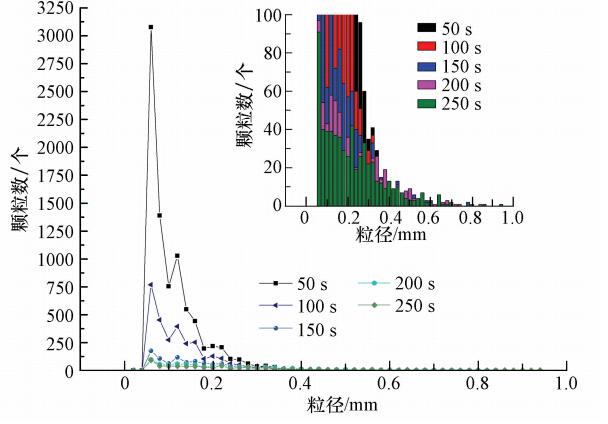
　　如圖 2所示，反應體系經過快速攪拌段進入慢速攪拌段后，絮體顆粒數目迅速下降，由最初視野范圍內的8000左右降至700左右，顆粒團聚現象明顯;同時絮體顆粒的平均粒徑大小迅速上升，由平均粒徑0.09 mm左右迅速升至0.23 mm左右.從時間分布上看，絮體生長階段在整個反應過程中所占比例不大，絮體生長速度快.

圖 2 絮體生長過程

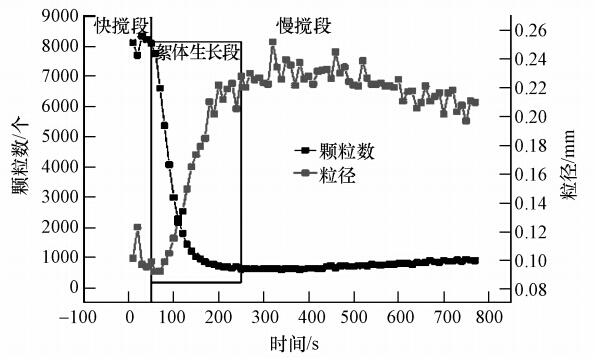
　　圖 3顯示的是絮體在生長過程中幾個時間點分布情況.從圖中可以看出，進入絮凝階段后，小粒徑顆粒迅速降低，大顆粒數目則明顯增多，分布圖形由高峰逐漸向低峰發展;同時，由于顆粒之間的團聚，顆粒粒徑范圍逐漸增大，即峰寬逐漸變大.在此需要說明的是，受到相機分辨率以及鏡頭分辨率等因素影響，小顆粒在圖片中的識別能力有限.

圖 3 絮體分布變化過程

　　4.2 絮體生長的多重分形特征

　　圖 4是相應的各取樣時間點絮體生長的多重分形譜變化情況.從此圖可以很直觀的看出多重分形譜在整個絮體生長段的變化，f(α)max逐漸降低，譜寬逐漸變大，絮體的多重分形譜從左勾狀曲線逐漸變化為右鉤狀曲線.

圖 4 絮體生長的多重分形譜

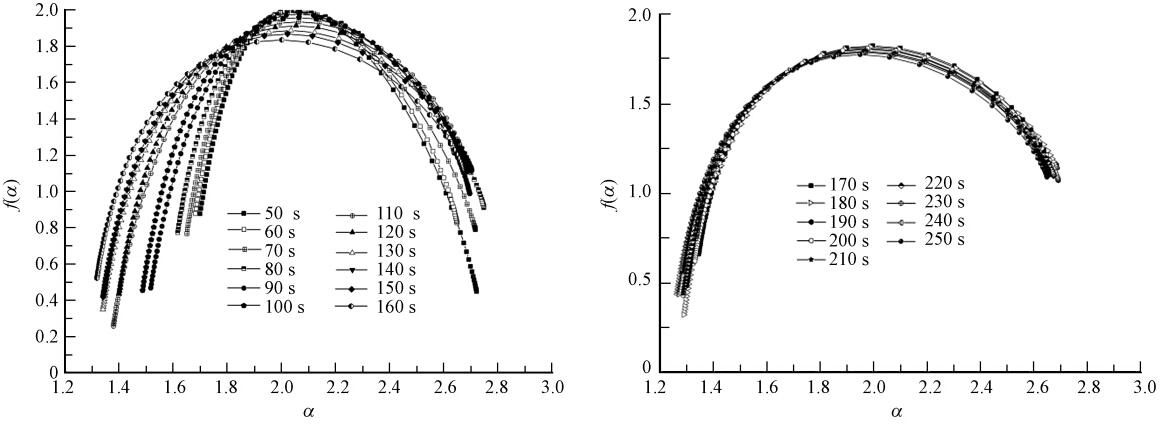
　　圖 5的部分數據顯示出了多重分形譜中f(αmax)、αmax、f(αmin)、αmin、Δf(α)、Δα等特征參數隨絮體生長的變化，表 1顯示的是絮體群生長過程中部分采集點照片的多重分形譜參數數據.可以看出，f(αmax)在50~130 s范圍內上升明顯，由0.4469上升為1.2097，140 s后表現穩定;f(αmin)在絮體生長前段由0.8768下降到0.2568，后端亦是在一定幅度內波動.這說明小概率對象即大粒徑絮體的數量在增加，大概率對象即小粒徑絮體的數量在減小.由Δf(α)= f(αmax)-f(αmin)的變化可知，Δf(α)由最初的-0.4299迅速增大到0.8679，隨后始終維持在一個較高水平.在70 s之前，Δf(α)<0，此時在整個體系中以小粒徑顆粒在顆粒分布占據主導地位;此后Δf(α)轉而大于0，并持續上升，說明大粒徑顆粒所表示的小概率顆粒在顆粒分布中逐漸搶占主導地位;130 s后Δf(α)表現相對穩定，說明大概率和小概率顆粒的數目比相對穩定.圖 3中表現出的分布情況也顯示出150 s、200 s和250 s之間的波峰和波谷比例已相對穩定.

　　圖 5 絮體生長f(αmax)、αmax、f(αmin)、αmin、Δf(α)、Δα變化

　　在整個反應進程中，αmax表現出相對平穩特征，這是由于αmax表示小概率顆粒，體現了最大粒徑顆粒在絮體分布中所占比例始終保持平穩;而大概率顆粒所代表的αmin呈現出明顯下降趨勢，由1.7降至1.3左右，體現了小顆粒在絮體生長段的聚集過程.Δα在整個生長段則表現出穩步上升的趨勢，由1.0213至1.3659.根據多重分形理論，Δα=αmax-αmin反映了概率分布范圍的大小，概率分布愈不均勻，相應的譜寬會越大;也就是說，Δα在絮體生長的過程中的增大，說明絮體粒徑范圍在擴大，概率分布變得越來越不均勻.從圖 3中也注意到絮體分布的峰寬逐漸增加.具體參見污水寶商城資料或http://www.bnynw.com更多相關技術文檔

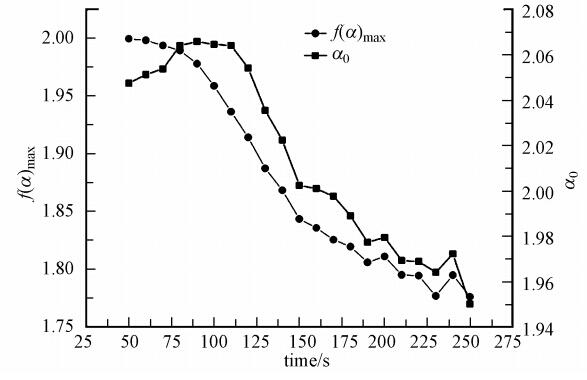
　　圖 6所示的是在多重分形譜中f(α)max、α0在絮體生長進程中的行進趨勢.根據多重分形理論的性質，當q=0時，D0為簡單維數，此時對應于f(α) max，與α0一起反映了最或然子集的性質，即反映了絮體群的整體幾何特征.結合表 1的數據，由于絮體在生長初期會經過碰撞簡單的結合在一起，α0在最初的30s內處于上升狀態，從2.0474升至2.0658，這說明絮體群整體的奇異程度在上升;而后處于持續下降的過程，至絮體生長段末α0降至1.9501，這是因為絮體顆粒數目迅速減少并且絮體開始團聚并相互擠壓，使絮體群的整體奇異性下降，并且由于顆粒數目的降低和絮體群空間占有率下降，f(α)max伴隨絮體的生長而呈下降態勢，由1.9995降至1.7762.

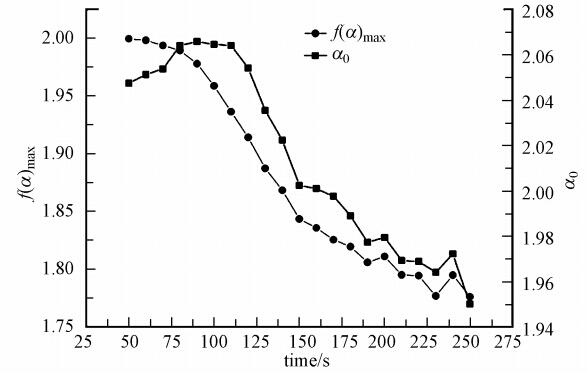
　　圖 6 絮體生長f(α) max、α0變化

　　表1 部分絮體照片的多重分形譜參數

　　結合圖 2，發現絮體生長段的多重分形特征參數變化并非隨平均粒徑的持續增大和顆粒數的持續減小而呈現持續的變化特性，如圖 5中f(αmax)、f(αmin)、αmin、Δf(α)、Δα在110~130 s之前變化顯著，而后出現上下波動或變化變緩的現象，圖 6中α0則出現先上升后下降的現象.這些不單單是由于絮體幾何形態發生變化，也與絮體分布特征的變化密切相關.如圖 3中所顯示的情況，絮體在150 s后的分布變化較之150 s之前的變化已經非常小，150 s之前，絮體主要以小顆粒碰撞聚集為主，表現為f(αmax)、f(αmin)、αmin、Δf(α)、Δα等參數的迅速變化;150 s之后絮體團族之間的聚集增多，較大粒徑顆粒出現，小顆粒進一步減少，這時的絮體概率分布不會出現太大的變化，但會向右緩慢發展.

　　5 結論與展望

　　通過對在絮凝生長過程中連續采集的絮體圖片的分析研究發現，多重分形譜及其特征參數可以定量描述絮體在成長過程中的絮體形態和分布的動態變化情況，從而獲取更多的絮體成長信息.當小顆粒進入到絮凝階段，多重分形譜圖由左勾狀轉變為右鉤狀，體現了絮體由小顆粒聚集為大顆粒的變化過程.Δα逐漸增大，表現出絮體分布的不均勻程度變化過程;Δf(α)的數值由負轉正的變化指示了絮體群落中絮體的主導地位變化;簡單分形維數f(α)max則逐漸下降.

　　絮體形態和分布特征的變化是絮凝過程中的重要現象，對其定量化有助于促進絮凝動力學研究及絮凝機理的完善.結合絮凝劑的反應機理和流體在不同條件下的紊動耗散規律，多重分形分析可揭示絮體的動態絮凝行為特征，為絮凝的過程控制提供重要的參考數據，更多相關內容正在進一步研究中.