1 引言

　　通過數學模型對污水處理的生化過程進行模擬分析一直是污水處理運行與管理領域的研究熱點.20 世紀 50 年代以來，國外一些學者把反映生化過程機理的微生物生長動力學引入污水處理領域.20世紀 80年代末，國際水協會(IWA)提出的活性污泥 1號模型(ASM1，Activated Sludge Model No. 1)取得了很大的成功，是早期較為完善的污水處理數學模型研究之一.通過模擬計算，使污水處理的設計和運行更加理論化和系統化，提高了人們對污水生物處理過程的認識，不僅節省了大量的經濟成本，而且提高了污水處理相關工作的質量和效率.

　　然而，隨著污水處理工藝及設備設施的日漸復雜，活性污泥數學模型在污水處理廠的實際應用中具有一定的局限性.一方面，數學模型的建立過程比較復雜，需要對水質組分及動力學參數進行測定，大部分污水廠缺乏這方面的基礎有效數據;另一方面，污水處理過程實際上是一個十分復雜的由物理、生物、化學等因素協同作用的過程，最終的處理效果不僅與決定其生物反應的一系列特征相關，同時還受大量不確定因素的影響，而活性污泥數學模型還遠未將這些因素考慮在內，這在一定程度上降低了模型預測的精確性和實際應用價值.

　　對此，筆者提出可通過基于數據驅動的黑箱模型對污水廠處理效果進行模擬預測.然而污水處理過程中去除污染物的種類很多，每種類型污染物都有其獨特的去除機理和影響因素，因此，僅通過建立一個黑箱模型就對所有指標進行預測勢必無法保證準確性.綜合考慮，本研究將黑箱模型主要用于污水處理脫氮工藝模擬分析，主要基于以下幾方面原因：①污水廠出水總氮是評判其工藝水平和運行水平的重要指標之一，對于一般水廠而言要保持出水總氮平穩達標，存在一定的技術難度和較大的調控空間;②對于傳統反硝化脫氮的機理及影響因素已研究的較為透徹，因此，可以很好地確定對脫氮效果有顯著影響的參數，同時這些參數在一般污水廠都有大量的實際數據;③隨著未來污水處理標準的日益提高，如何能保障前端脫氮效果，對后續深度處理工藝的成本控制有重要影響.

　　基于此，本文采用BP神經網絡與馬爾可夫鏈的組合預測模型，首先通過BP神經網絡模型對北京某大型污水處理廠實際進出水數據和工藝參數進行粗略擬合;其次，利用馬爾可夫鏈對擬合結果及誤差進行狀態劃分以進一步提高預測精確度;最后，運用基于BP神經網絡與馬爾可夫鏈的組合模型預測分析該廠的實際出水水質.

　　2 BP神經網絡和馬爾可夫鏈模型的構建

　　2.1 BP神經網絡模型構建

　　神經網絡模型是以神經元的數學模型為基礎來描述的，是一種按誤差逆向傳播算法訓練的多層前饋網絡，它由網絡拓撲、節點特點和學習規則來表示，能在未知被構建對象和輸入參數的數學關系式的情況下，通過學習和貯存大量的輸入-輸出模式關系，自適應地獲取輸入與輸出的非線性映射關系.這其中又屬BP 神經網絡的應用最為普遍，它使用最速下降法，通過反向傳播來不斷調整網絡的權值和閾值，使網絡的誤差平方和最小.應用 BP 神經網絡一般包括4個基本步驟：①確定網絡結構形式;②收集訓練和測試樣本;③進行網絡模型訓練;④利用訓練后的網絡進行應用計算.

　　神經網絡模型的模擬過程中會應用到大量的樣本訓練和測試數據，一般污水廠生產運行過程中會產生大量數據，但這些數據大部分是由人工或儀表檢測而來，受取樣、化驗操作、瞬時波動、儀表等因素影響，這些數據經常存在誤差和波動.用這樣的數據進行神經網絡的訓練，往往會導致預測結果在一定范圍內隨機波動，降低了預測的準確性.馬爾可夫鏈恰能有效地預見并消除由系統隨機性而產生的預測誤差.因此，通過建立神經網絡與馬爾可夫鏈的組合預測模型，將二者進行優勢互補，能夠得到更為準確的預測結論

　　2.2 馬爾可夫鏈模型構建

　　馬爾可夫鏈是根據俄國數學家馬爾可夫發現的系統狀態轉移規律，分析隨機事件未來發展趨勢及可能結果的一種預測方法其實質是對于事件發生的概率進行預測，根據目前狀況來預測其將來時刻變動狀況.馬爾可夫鏈預測主要分兩個過程：一是確定馬爾可夫鏈的狀態空間;二是要通過計算確定狀態轉移概率與狀態轉移矩陣.

　　在事件發展變化過程中，狀態Ei經過k步轉移到狀態Ej的轉移概率Pkij為：

　　式中，Mi表示狀態Ei出現的總次數，mkij表示狀態Ei經k步轉移到狀態Ej的次數，m為劃分的狀態數目.

　　對于BP神經網絡模擬預測的結果，通過馬爾可夫鏈模型可以分析其誤差的波動范圍，并且預測波動的發展趨勢，通過誤差的狀態轉移概率矩陣對BP神經網絡預測的結果進行進一步的精細優化.馬爾可夫鏈是一個典型的無后效應隨機過程，即模型在時刻t的狀態只與它的前一個時刻t-1的狀態條件相關，與以前的狀態條件獨立.

　　在污水處理過程中，下一時刻污染物濃度變化情況只與當前時期(8~12 h)的系統狀態有關，而與之前的狀態無關.此外，該模型的最終預測結果不是一個具體數值，而是生成一組不同概率的預測區間值，該方法可從一定程度上彌補因化驗產生的數值誤差，提高預測準確度.

　　3 污水處理廠脫氮效果模擬預測分析

　　本文采用北京某大型污水處理廠的實際生產數據為實驗依據，該廠設計日處理規模100萬m3 · d-1，其主體工藝采用A/O法去除有機污染物(COD)和總氮(TN)，同時還通過投加化學藥劑來去除總磷(TP)，最終出水主要指標可穩定達到《城鎮水污染物排放標準》(GB18918)中的一級B標準.

　　由于污水處理過程中每種類型污染物的去除都有其各自的原理和特點，因此，其影響因素也各不相同.例如，對于BOD、COD等有機指標，一般水廠均能較徹底的去除，其出水的殘留值主要與原水中的溶解性不可降解有機物有關.再例如懸浮物指標，主要與沉淀單元的水力負荷和狀態點有關，而與其它水質指標關聯不大，等等.其中，總氮是污水中的主要污染物之一，其去除機理和影響因素目前研究的較為明確，因此，本文主要以脫氮工藝模擬為研究對象，對該廠出水總氮進行數學模擬分析.

　　3.1 基于BP神經網絡的污水廠脫氮效果模擬

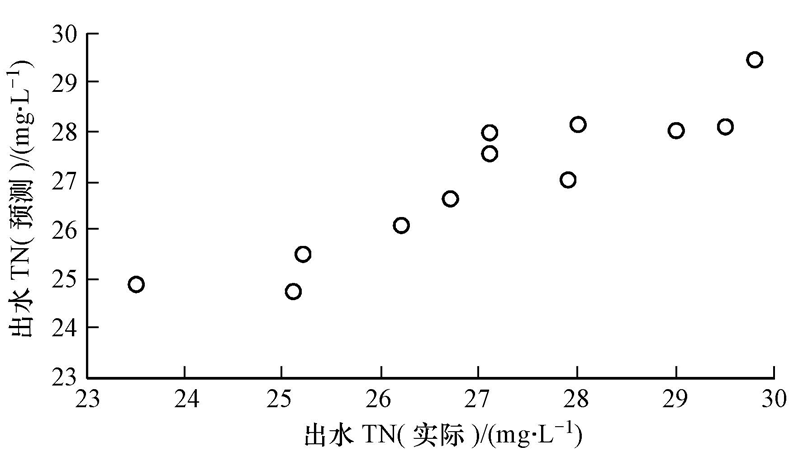
　　以該廠2013年全年數據為基礎，共收集了365組樣本集，其中250組作為訓練集，115組作為測試集.試驗工具采用新西蘭懷卡托大學開發的WEKA數據挖掘應用平臺，BP神經網絡輸入層節點數為 8，分別表示進水流量、生物反應池溫度、進水BOD、進水COD、進水TN濃度、進水NH+4-N濃度、生物反應池MLSS濃度、生物反應池MLVSS濃度;輸出層節點為出水TN濃度，隱藏層數取1，迭代次數為500，采用不同的隱含層節點數分別對網絡進行訓練，當隱含層節點數取4時，神經網絡訓練誤差最低(平均誤差0.073).利用訓練后的模型，以2013年各月的月均參數值為輸入量(表 1)，模擬各月月均TN值，模擬結果與真實值的線性相關度為0.921(圖 1).

　　北京某污水處理廠2013年1—12月主要運行數據

圖1 神經網絡模型擬合結果 

       利用訓練后的神經網絡對該廠2014年1—12月數據進行模擬預測，最終模擬值與實際值對比情況如圖 2和表 2所示.從表 2可以看出，12個月的數據模擬誤差范圍為±10%，有3次模擬結果低于實際值，9次高于實際值.其中，最小誤差為0.79%，最大誤差為9.49%.

　　表2 污水處理廠實際出水水質及BP網絡計算擬合值

       3.2 基于馬爾可夫鏈的預測結果修正模型 3.2.1 馬爾可夫狀態區域劃分

       馬爾可夫鏈的預測精度主要由轉移矩陣決定，為了構造轉移矩陣，首先需要合理劃分誤差狀態區間，一般以樣本-均方差方法來確定.以樣本的均值 為中心，標準差s=

為標準進行分組.一般可將數據序列分為：(x-s，x-0.5s)、(x-0.5s，x+0.5s)、(x+0.5s，x+s)等幾組.

　　從表 2可以看出，模擬值與實際值誤差在-10%~5%之間，誤差平均值為x=-2.5，標準差為s=4.28.根據均值-標準差分級方法，通過BP模擬結果的誤差均值和標準差，可將馬爾可夫狀態區域劃分為4種狀態：a[-10%，-5%]，b[-5%，0]，c[0，+5%]，d[5%，10%]

　　3.2.2 污水廠出水總氮BP擬合結果一步轉移概率矩陣

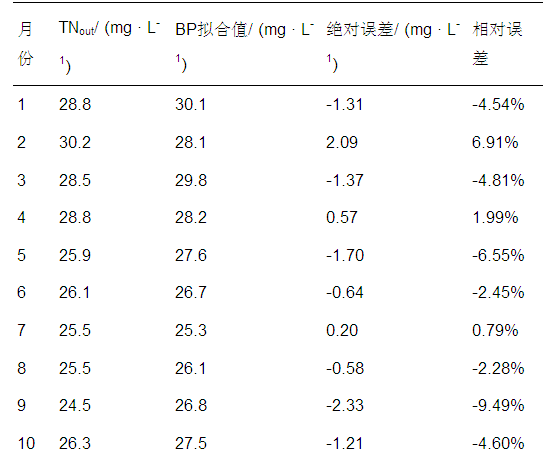
　　對于馬爾可夫鏈，描述其概率性質的重要的量是轉移概率矩陣.把轉移概率Pij=(n，n+k)記為Pij，當k=1時，Pij(1)稱為1步轉移概率，記為Pij.設 P 表示一步轉移概率Pij(k)所組成的矩陣(式(2))，且狀態空間E={1，2，…，n}，則 P 稱為系統狀態的一步轉移概率矩陣.

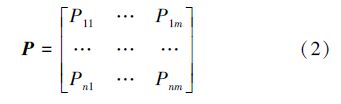
　　根據之前的3種區域狀態劃分，pij為由狀態i轉向狀態j的頻數，如pab表示當前誤差在a狀態，下一組模擬誤差在b狀態的頻數，其余以此類推.設：

　　那么由狀態i轉向狀態j的轉移概率為fij≈pij/pi，(i=1，2，…，n)，這樣便可得到BP模擬出水TN誤差的一步轉移概率矩陣，具體如表 3和式(3)所示.

　　表3 污水處理廠出水水質預測結果的馬爾可夫狀態轉移表

　　3.2.3 馬氏性檢驗

　　檢驗隨機過程是否具有馬氏性是應用馬爾科夫鏈模型的必要前提，通常離散序列的馬爾科夫鏈是用χ2 統計量來檢驗的.

　　j表示(nij)q×q的第j列之和同各行各列的總和的比值，Pij表示狀態i轉到狀態j的概率，計算公式如下：

　　統計量服從自由度為(q-1)2的χ2分布.選定置信度α，查表得χ2α((q-1))2，令：

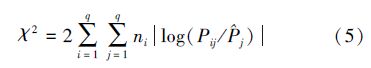
　　若χ2>χ2α((q-1))2，則{ri，i=T}具有馬氏性.對該廠12個月的狀態序列做馬氏檢驗.根據表 3再結合步長為1的一步轉移概率矩陣 P，可算得統計量χ2=32.14，給定置信度α=0.05，查表可得分為點χ2a(4)=27.85.由于χ2>χ2α((q-1))2，故這組序列滿足馬氏性.

　　3.2.4 2015年1—5月出水總氮預測

　　根據2014年1—12月模擬結果，通過馬爾可夫鏈預測模型，得到2015年1—5月出水總氮狀態轉移表，結果如表 4所示.其中，參考2014年12月的模擬誤差，初始向量為[0.17，0.33，0.33，0.17].

　　表4 2015年1—5月出水TN預測狀態向量

 　　綜上，得出2015年1—5月出水的最終預測結果(表 5).馬爾可夫鏈改進后的預測結果是不通過概率下的區間范圍值，符合污水廠出水水質和檢測結果在一定程度呈隨機變化的特性，通過最大概率區間預測值可以很準確地預測實際出水水質范圍.從該廠2015年1—5月的模擬預測結果可知，出水的實際水質均符合最大概率區間內的預測范圍值，表明基于 BP神經網絡與馬爾可夫鏈的組合預測模型具有較高的精度，可應用于污水處理的水質模擬.

　　表5 污水處理廠2015年1—5月出水實際值、BP擬合值與馬爾可夫改進值對比情況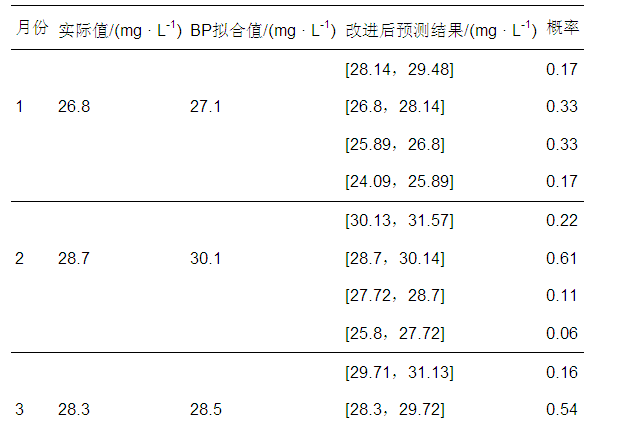 　　　　　

　　4 結論

　　1)污水處理過程是多種復雜生物化學反應綜合作用的結果.本文所采用的模擬方法和預測模型是對傳統污水處理數學模型的一種補充，即通過數據挖掘手段，采用基于BP 神經網絡與馬爾可夫鏈的組合預測模型，充分挖掘出數據中的變化規律與擬合趨勢，恰好彌補了傳統數學模型的不足.

　　2)通過對北京某污水處理廠實際數據分析計算表明，BP神經網絡模型結合馬爾可夫鏈組合模型具有很好的適用性，能夠準確預測出水水質范圍.在不掌握生物反應機理模型參數或缺乏數據的情況下，為污水處理廠水質模擬提供了一種新的途徑.具體參見污水寶商城資料或http://www.bnynw.com更多相關技術文檔。

　　3)本方法尤其適合于運行工藝和進出水水質相對穩定，且具有大量歷史數據積累的水廠.由于污水處理過程影響因素的多樣性和不確定性，對于不同類型的水廠，在具體建模時還應結合實際情況，在神經網絡輸入層節點(即污水處理的影響因素)選取和馬爾可夫狀態區域劃分方面進一步研究分析.