1 引言(Introduction)

　　厭氧氨氧化(Anaerobic Ammonia Oxidation, Anammox)技術作為近年來成功研發的新型生物脫氮技術, 因具備能耗低、無需外加碳源、產泥量較少等優點受到人們的密切關注(胡寶蘭等, 1999;Jetten et al., 1997).目前, 該技術在荷蘭、丹麥等國已成功運用于消化污泥壓濾液、馬鈴薯加工廢水及垃圾滲濾液等廢水處理過程(Li et al., 2015a;唐崇儉等, 2010).厭氧氨氧化是指厭氧氨氧化菌在厭氧或缺氧條件下, 以NH4+-N為電子供體, NO2--N為電子受體, 將NH4+-N、NO2--N轉化為N2的生物氧化過程(曹天昊等, 2015).在厭氧氨氧化過程中, 約有11%的總氮會轉變NO3--N, 造成NO3--N的累積;同時, 在實際含氮廢水中, 也往往存在有機物(Chen et al., 2016;Li et al., 2015b).NO3--N和有機物均可被反硝化細菌利用, 但另一方面, 反硝化細菌也會同厭氧氨氧化菌競爭作為電子受體的NO2--N, 從而導致厭氧氨氧化菌脫氮能力的降低.目前, 已有學者(魏思佳等, 2016)報道, 厭氧氨氧化菌可以與其他細菌共存, 如反硝化細菌, 這也使得利用厭氧氨氧化與反硝化協同作用實現同步脫氮除碳處理含氮和COD的廢水成為可能.當前, 已有較多研究表明, COD與COD/TN都會影響厭氧氨氧化脫氮性能, 另一方面, 作為厭氧氨氧化基質的NH4+-N、NO2--N也是影響其工藝穩定性的重要因素(操沈彬等, 2013;李媛, 2014).Chen等(2016)發現, 當進水COD<99.7 mg·L-1時, 厭氧氨氧化脫氮能力有所提升, 當COD達到284.1 mg·L-1時, 厭氧氨氧化完全被抑制;魏思佳等(2016)在保持進水COD 300 mg·L-1、NO2--N 145 mg·L-1條件下, 通過改變NH4+-N進水濃度發現, 要保持總氮去除率>94%, COD/NH4+-N值要大于3.25, NH4+-N/NO2--N值要小于0.63, 但未能考慮進水COD、NO2--N等因素變化的影響.因此, 如何快速、準確地選取工藝條件實現厭氧氨氧化與反硝化協同同步脫氮除碳, 采用傳統方法仍較為復雜困難, 亟需新的解決手段.

　　智能算法作為當前一個新興領域, 因具有無需準確的數學模型、強大的推理機制, 以及各智能算法之間良好的兼容性和相互彌補性, 對于解決復雜的實際問題變得越來越熱門(向娜, 2012).在廢水處理領域中, 智能算法的出現很好地解決了廢水處理過程中具有的約束性、非線性、不確定性和建模困難等問題, 目前已廣泛應用于水質監測、參數優化、模擬建模、工藝控制等方面(韓偉, 2015;Badrnezhad et al., 2014).BP算法是目前應用最廣泛的神經網絡學習算法, 它通過隱含層將輸入數據從輸入層變為網絡輸出量, 實現空間映射.通過對網絡輸出和期望輸出進行比較, 根據梯度下降法調整權重, 至網絡輸出與期望輸出的均方差達到最小, 使得BP神經網絡具有良好的非線性映射能力(黃明智, 2010).目前, 針對基于BP神經網絡的軟測量模型已經有了大量研究, 其在廢水處理中的運用也越來越廣(韓偉等, 2014).

　　在工程中經常會遇到如實現厭氧氨氧化與反硝化協同同步脫氮除碳此類的多準則或多設計目標下的設計和決策問題, 這些目標往往相悖, 要找到滿足這些目標的最佳設計方案, 就要解決多目標和多約束的優化問題(高媛, 2006).傳統的多目標優化方法, 如加權法、約束法、混合法、目標規劃法、最大最小法等, 因存在主觀性大、優化進展不可操作的缺點, 在處理高維數、多模態、非線性等復雜問題上存在許多不足(余廷芳等, 2013).在2002年, Deb等(2000)提出了非常經典的快速非支配排序遺傳算法NSGA-Ⅱ, 所求的最優解集能夠很好地逼近Pareto前沿, 所采用的距離擁擠機制使得最優解集擁有良好的分布, 因其良好的綜合性能而被廣泛應用到實際系統設計中(Huang et al., 2016).韓偉(2015)基于神經網絡和NSGA-Ⅱ設計出的一套針對造紙廢水的控制-預測-優化系統, 為智能算法在造紙廢水厭氧處理的應用提供了幫助.對于過程更為復雜的厭氧氨氧化與反硝化協同問題卻很少有人涉及.

　　本文以厭氧氨氧化與反硝化過程為研究對象, 以NH4+-N和COD去除效果同時最大化為目的, 通過建立起的PCA-BP預測網絡和NSGA-Ⅱ優化網絡, 對厭氧氨氧化與反硝化協同實現同步脫氮除碳過程進行優化, 確定進水NH4+-N、NO2--N和pH等參數的最佳取值.以期為此類廢水處理過程存在的協同優化問題和智能算法的實際應用提供參考和指導.

　　2 材料與方法(Materials and methods)2.1 實驗裝置和工作條件

　　實驗裝置采用如圖 1所示的上流式厭氧污泥床(Up-flow Anaerobic Sludge Bed, UASB)裝置, 其材質為有機玻璃, 反應器有效容積為25.12 L, 其中, 反應區容積為18.12 L, 沉淀區容積為7 L.反應器外包裹黑布以防止光氧化菌的影響.模擬廢水由BT600-2J型蠕動泵經反應器底部布水系統進入反應器, 通過控制泵的轉速控制廢水停留時間, 氣、泥、水混合液通過設在反應器頂部的三相分離器分離, 出水由溢流堰排出.水質參數在線監測系統由在線pH儀表(美國哈希公司, GLI MODEL33)和濕式氣體流量計(LML-1型)組成.實驗所用接種污泥為廣州某污水廠厭氧段污泥, 反應器經6個月成功啟動并達到穩定狀態.在HRT為8 h時, 氨氮、亞硝酸鹽氮和總氮的去除負荷分別為0.56、0.76和1.32 kg·m-3·d-1.在穩定階段, 氨氮去除、亞硝酸鹽氮去除與硝酸鹽氮的生成比為1：(1.25±0.03)：(0.28±0.02), 接近于理論值.

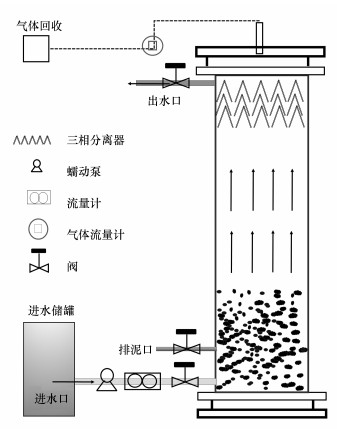
　　圖 1 UASB反應器示意圖

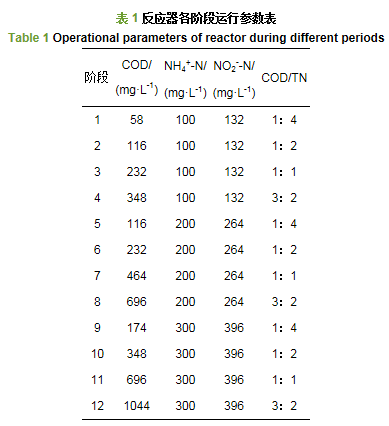
　　實驗采用人工自配廢水, 主要成分為(mg·L-1)：KH2PO4 10, CaCl2·2H2O 5.6, MgSO4·7H2O 300, NaHCO3 1250, 微量元素濃縮液各1.25 mL, 具體組分參見Wang等(2009)方法投加.NH4+-N、NO2--N和COD由NH4Cl、NaNO2和葡萄糖按需提供, 控制進水NH4+-N與NO2--N物質的量比為1：1.32, 用碳酸氫鈉調節進水pH在7.3~7.8之間.進水NH4+-N、NO2--N和COD的水質指標見表 1.實驗期間, NH4+-N測定采用納氏分光光度法, NO2--N測定采用萘乙二胺分光光度法, COD測定采用重鉻酸鉀滴定法.

　　2.2 PCA-BP模型的建立

　　BP(Backpropagation)神經網絡是一種具有連續傳遞函數的多層前饋人工神經網絡, 以均方誤差最小化為目標, 其訓練方式采用誤差反向傳播算法, 通過不斷修改網絡的權值和閾值, 最終達到高精度擬合數據的非線性不確定性數學模型(劉春艷等, 2013).在實際使用過程中, 由于針對厭氧氨氧化的廢水處理控制過程是一個包含多變量、多目標、多層次的有著海量信息的復雜系統, 其各種水質參數之間存在強烈耦合和關聯的情況, 因此, 本文采用PCA(Principal Component Analysis)揭示各過程變量間的線性相關關系, 將多個相關變量轉化為少數幾個相互獨立變量, 實現輸入數據降維, 即輔助變量的精選(劉博等, 2015;冉維麗等, 2004).

　　PCA是一種統計相關分析技術, 是作為輸入數據集降維和揭示變量間線性相關關系的工具(Yao et al., 1997).主元分析的基本思想是在保證數據信息丟失最少的原則下, 對高維變量空間進行降維處理分析, 使低維特征向量中的主成分變量能保留原始變量的特征信息，同時消除冗余信息(Jolliffe et al., 2016).

　　基于PCA-BP神經網絡的預測模型的主要建模步驟如下：①原始數據的獲取, 通過改變進水條件, UASB厭氧反應器成功運行150 d, 在此期間獲得進水NH4+-N、NO2--N、COD、pH和出水NH4+-N、COD、pH等多項指標;②數據預處理, 包括數據異常值的剔除和歸一化操作, 其目的在于確保模型的輸入和輸出值的統計分布大致均勻, 從而提高模型的運行精度及運行速度;③將步驟②獲得的數據利用PCA進行數據降維, 通過計算累計方差貢獻率, 確定主成分個數, 組成新的數據樣本矩陣實現數據降維;④利用步驟③中獲取的新的樣本數據, 利用BP算法建立起預測模型;確立BP神經網絡的初始權值和閾值, 并通過“試錯法”確定隱含層神經元數, 進行訓練與測試;⑤數據可視化輸出, 將最終得到的結果以圖表形式輸出以供分析.

　　2.3 基于PCA-BP和NSGA-Ⅱ的多目標優化模型

　　NSGA-Ⅱ算法是基于NSGA(Non-Dominated Sorting in Genetic Algorithms)算法進行改進, 用于解決多目標優化問題(Deb et al., 2000).針對NSGA-Ⅱ算法的建立需要關于優化目標問題的數學模型, 對于厭氧氨氧化等廢水處理工藝而言, 由于各參數量與優化目標之間往往是非線性且復雜的關系, 傳統的機理建模無法做到, 本文中通過采用PCA-BP神經網絡很好地模擬出各參數量與優化目標量之間的關系, 將該模型代替傳統的數學模型用于NSGA-Ⅱ算法中解決厭氧氨氧化處理過程中存在的多目標優化問題, 最終建立起基于PCA-BP和NSGA-Ⅱ相結合的多目標優化模型.本文中模型均在Matlab2015b軟件平臺、Windows10環境下建立.NAGA-Ⅱ算法的基本流程如圖 2所示.

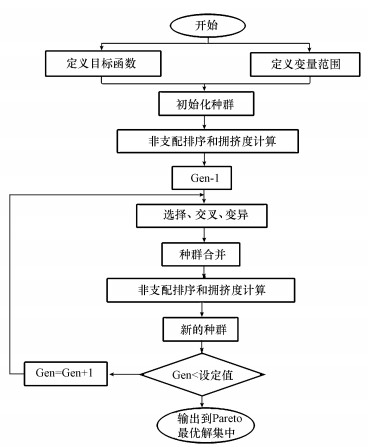
　　圖 2優化模型流程示意圖

　　針對厭氧氨氧化與反硝化協同實現同步脫氮除碳, 建立如下優化模型, 目標函數如式(1)和(2)所示, 約束條件見式(3).

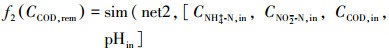
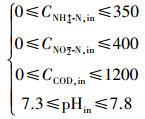
　　式中, net1、net2分別為基于PCA-BP算法建立的NH4+-N和COD去除濃度預測模型, CNH4+-N, in、CNO2--N, in、CCOD, in、pHin分別代表進水NH4+-N、NO2--N、COD和pH, 進一步選取NSGA-Ⅱ參數為：種群數量100、交叉概率0.4、變異概率0.05、最大進化代數500.

　　2.4 原始數據的采集及PCA處理

　　UASB反應器成功啟動之后進行數據采集工作, 通過改變進水條件, 反應器連續運行工作150 d.采集到的數據剔除明顯異常值后利用拉依達準則剔除離群值, 共得到144組元數據.實驗選取的模型輸入量包括進水NH4+-N、NO2--N、COD和pH 4項操作變量, 以COD和NH4+-N去除濃度作為模型輸出變量.為消除量綱影響, 提高模型運算速度, 利用公式(4)對原始數據進行歸一化處理：

　　式中, S(i)為數據集中的一組數據;max(S)為數據集中最大的一組數據;min(S)為數據集中最小的一組數據.

　　經歸一化處理后的數據使用MATLAB 2015b軟件進行PCA降維操作, 通過分析各個變量的相關性降低輸入數據維數, 去除冗余信息及減少BP的計算量.處理結果如圖 3所示, 雙標圖(圖 3a)顯示了輔助變量與樣本點之間的多元關系, 連接原點和各變量的直線稱為“向量”, 其在某一主成分上的投影表明該變量對該主成分的重要程度, 同時也體現了該主成分對該變量的解釋程度(劉博等, 2015).從圖 3a中變量的矢量長度可以看出, 進水NH4+-N、NO2--N濃度和進水pH都是十分重要的影響變量, 相對來說, 進水COD的影響較小.從圖 3b可以看出, 第一主成分的方差貢獻率為71.58%, 第二主成分的方差貢獻率為17.21%, 總貢獻率為88.79%, 屬于中等偏上的擬合度水平;根據主成分的一般選則標準, 累計方差貢獻率≥85%的前k個主成分能夠包含絕大部分信息, 后面的其他成分則可以舍棄, 這里原來的4項指標即可由這2個主成分代替.

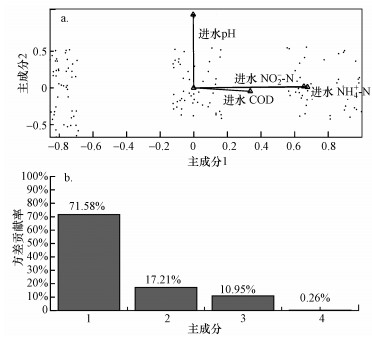
　　圖 3雙標圖(a)和方差貢獻率(b)

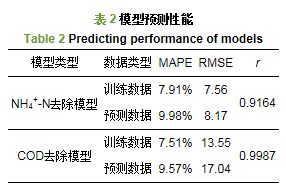
　　本文選取3個評價指標用以表征模型預測性能, 其中, MAPE(Mean Absolute Percent Error)是所有相對誤差的絕對值求和的平均值, 能從整體上更好地反映預測值的實際情況;RMSE (Root Mean Square Error)是觀測值與真實值偏差的平方與觀測次數n比值的平方根, 可以說明樣本的離散程度, RMSE值越小, 說明預測模型描述實驗數據的精確程度越高, 反之亦然;r(correlation coefficient)反映了預測值與實際值線性關系的強弱, r值越接近于1, 代表預測值與實際值越接近(劉林等, 2017).

　　3 結果與討論(Results and discussion)3.1 PCA-BP模型預測仿真

　　結合上文, 原始數據經歸一化和PCA處理后, 分別建立起基于BP神經網絡的NH4+-N和COD去除濃度預測模型, 其中, 輸入層為進水NH4+-N、NO2--N、COD和pH, 輸出層分別為NH4+-N和COD去除濃度, 通過試錯法選用5個節點作為隱含層節點, 模型的拓撲結構最終為4-5-1.從實驗樣本中選取120組數據作為訓練樣本, 24組數據作為檢驗樣本.值得注意的是, 模型的訓練樣本和檢驗樣本的選取都應包含多種條件.選用函數tansig和logsig作為隱含層和輸入層神經元的傳遞函數, 選用函數trainlm作為訓練函數.網絡的學習速率為0.3, 學習動量常數為0.001, 目標誤差為0.015, 最大迭代為1000次.仿真結果如圖 4和表 2所示.

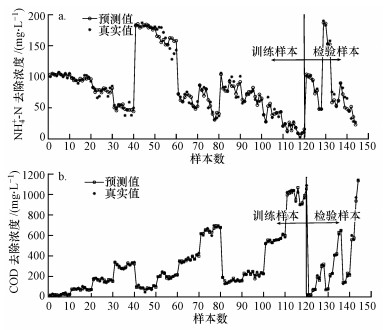
　　圖 4 PCA-BP模型對NH4+-N (a)和COD (b)去除的仿真結果

　　從圖中可以看出, 模型預測值與實際真實值基本趨同.由表 2可知, 檢驗樣本中對NH4+-N去除濃度的預測值和真實值之間的平均相對誤差為9.98%, 均方根誤差為8.17, 預測數據與實際數據的相關系數為0.9164;而對COD而言, 其預測值與真實值之間的平均相對誤差為9.57%, 均方根誤差為8.17, 預測數據與實際數據的相關系數為0.9987.兩模型的平均預測誤差都在10%以內, 這表明BP神經網絡具有很好的預測能力及良好的非線性映射能力, 能夠作為NSGA-Ⅱ的目標函數.具體聯系污水寶或參見http://www.bnynw.com更多相關技術文檔。

　　3.2 基于PCA-BP和NSGA-Ⅱ的多目標優化的實現

　　模型優化結果如圖 5所示, 由圖中Pareto最優邊界點可以看出, 出水NH4+-N去除濃度和COD去除濃度之間存在或則這樣的關系：當出水NH4+-N去除濃度提高時, 出水COD去除濃度隨之下降, 反之亦然.為直觀地從數學模型角度解釋預測模型中NH4+-N去除濃度和COD去除濃度之間的線性關系, 運用MATLAB的聚類多項式線性擬合工具進行擬合, 出水NH4+-N去除濃度和COD去除濃度之間的聯系可以用四次多項式表示為式(5), 其可決系數R2為0.9963.

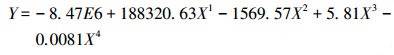
　　圖 5(Fig. 5)

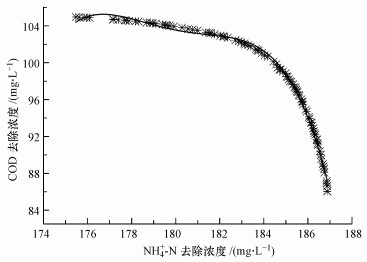
　　圖 5優化模型運行結果 Fig. 5 Results of the optimization model

　　表 3給出了部分Pareto最優邊界點和此進水條件下的實驗室出水真實測定值, 對比模型給出的模擬值與實驗真實值, 兩者差別不大, 表明本文所建立的多目標優化模型較為可靠, 能夠得到最優解集.圖 6給出了目標迭代過程中每一代進水NH4+-N、NO2--N、COD和pH參數的分布情況, 從圖中可以看出, 進水COD變化不大, 其值保持在106 mg·L-1左右, 進水pH分布于7.3~7.5之間, 進水NH4+-N與NO2--N均勻分布于280~320 mg·L-1和210~320 mg·L-1之間;進一步分析進水NH4+-N/NO2--N與出水NH4+-N去除濃度之間的關系(圖 7a), 發現隨著出水NH4+-N去除濃度增大, NH4+-N/NO2--N由0.95增大到1.50, 其表現為進水NH4+-N濃度增大, 而NO2--N濃度降低, 這可能是因為高濃度的NO2--N會抑制微生物活性, 相應的雖然NH4+-N濃度提升, 但低pH相應的低游離氨使厭氧氨氧化系統更為穩定(Jaroszynski et al., 2011);分析進水COD/NH4+-N與出水NH4+-N去除濃度之間的關系, 從圖中可以看出(圖 7b), 隨著出水NH4+-N去除濃度增大, COD/ NH4+-N由0.38下降到0.33, 可見要想使厭氧氨氧化反應器具有較優的脫氮效果, 控制進水COD與NH4+-N濃度比值是十分重要的.

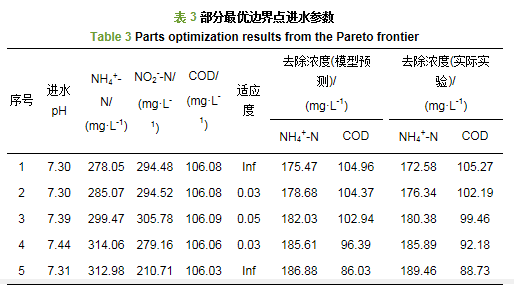
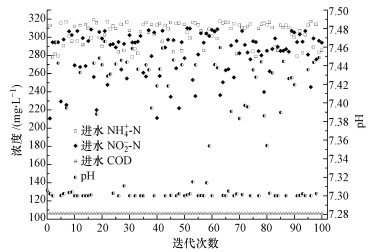
　　圖 6 Pareto最優邊界中各變量分布

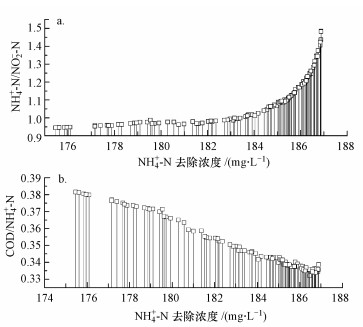
　　圖 7 NH4+-N/NO2--N (a)、COD/ NH4+-N (b)與NH4+-N去除濃度關系

　　4 結論(Conclusions)

　　1) 通過PCA降維操作處理模型輸入量, 分析各向量在某一主成分上的投影和矢量長度可知, 進水NH4+-N、NO2--N濃度和進水pH都是十分重要的影響變量, 相對來說, 進水COD的影響較小.

　　2) 通過PCA降維操作, 可以使模型輸入變量由4個降為2個, 去除冗余信息的同時, 可以減少BP的計算量.

　　3) 針對厭氧氨氧化過程中NH4+-N去除和COD去除雙項優化問題, 成功建立起基于PCA-BP的出水NH4+-N去除和COD去除預測模型, 模型測試數據與實際數據的相關系數分別為0.9164和0.9987, 且兩模型的平均預測誤差都保持在在10%以內.

　　4) 在出水NH4+-N去除和COD去除預測模型上, 利用NSGA-Ⅱ建立了厭氧氨氧化與反硝化協同實現同步脫氮除碳優化模型, 優化結果表明, 該模型給出的解決方案有效可行, 分析各進水參數之間的關系得出, 隨著出水NH4+-N去除能力的提升, 應當提高進水NH4+-N/NO2--N和降低COD/ NH4+-N的比值。(來源：環境科學學報 作者：謝彬)