1 引言
區域土壤重金屬污染評價是土壤環境研究的和污染防治的重要基礎目前對區域土壤重金屬污染程度的評價方法已有很多研究,如單因子指數法、地累積指數法、生態風險系數法等簡單指數法,內梅羅指數、加權綜合指數、生態風險綜合系數等綜合指數法,這些評價模型在土壤重金屬評價領域得到了廣泛應用.為了解決傳統的指數法評價難以描述土壤重金屬污染的不確定性問題,模糊數學方法在土壤重金屬污染評價領域得到廣泛的應用.核密度估計法不對數據的分布形式進行預先的假設,具有更廣泛的適用性,但目前核密度估計模型在自然科學上的應用不多,主要是集中在社會、經濟以及醫藥等領域.
不同評價方法各有應用特點,評價方法主要是掌握研究區域總體污染程度,但很少有學者對不同方法評價結果進行系統的總結與比較,即使有也僅僅停留在理論上的介紹,缺乏定量探討各方法評價結果的差異(范拴喜等,2010;郭笑笑等,2011).因此,本文以經濟快速發展的昆山市為例,采用簡單數理統計、正態模糊數法和核密度估計法對研究區土壤重金屬總體污染程度進行評價,從評價便捷性、結果的準確度與全面性方面揭示各方法的差異.
2 研究區概況
昆山市位于江蘇省東南部,上海和蘇州之間,地處東經120°48′21″~121°09′04″E,北緯31°06′34″~ 31°32′36″N,是上海經濟圈重要的新興工商城市,2013年人均GDP達2.89萬美元,連續9年被評為全國百強縣市之首.昆山市屬于典型的北亞熱帶季風氣候,年平均氣溫17.6 ℃,年平均降水量1200.4 mm,全市土壤分為水稻土、潮土、沼澤土、黃棕壤4個土類,水稻土在各類土壤總面積中占比最高,達93.8%.
3 數據來源和方法
3.1 數據來源
研究數據為2 km×2 km網格的土壤采樣測試數據,將研究區劃分成2 km×2 km的網格,每個網格作為一個采樣點,對于區域邊界上的破碎網格按照四舍五入來處理,共選取232個樣點.按照5點混合采樣法采集0~20 cm表層土壤樣品,四分法取分析樣品約1.5 kg.樣品經自然風干,挑除石礫和植物殘體,研磨過100目篩,并充分混勻以待用.

圖1 采樣點分布圖
本文側重研究不同方法下土壤重金屬污染程度評價結果的差異,較土壤重金屬綜合污染評估而言,單元素評估可以免去綜合污染的加權求和,能減少不同權重對結果的干擾.已有研究表明:作為水網地區的昆山市土壤As含量相對不高,空間分異程度也較小;Cd含量相對較高,空間分異程度也較大(萬紅友等,2006;鐘曉蘭等,2008).這兩種元素具有較強的代表性,能在污染評估結果中形成較為鮮明的對比,因此,本文選取As和Cd為代表元素進行研究.Cd采用分別加入濃鹽酸、濃硝酸在150 ℃的有孔電熱板上加熱反應、再加入HF-HNO3-HClO4置于200 ℃有孔電熱板上加熱消解后,采用ICP-MS法測定;As采用1 ∶ 1的王水沸水浴消解后用還原氣化-原子熒光光譜法進行測定.
3.2 研究方法
3.2.1 地累積指數法
地累積指數法通常稱為Muller指數,能很好地反映自然變化與人為活動因素對重金屬分布帶來的影響,它以研究區重金屬含量背景值為標準,是評價區域重金屬污染的重要污染指數.具體公式如下:
式中,Ci為土壤重金屬元素i的實測含量(mg · kg-1); Bi為元素i的區域背景值(mg · kg-1);k為修正系數,一般取為1.5.根據地累積指數值Igeo,將土壤重金屬污染程度劃分為5個等級.其中Igeo≤0時為0級,清潔;03時為4級,嚴重污染.
本文的重金屬含量背景值采用應用廣泛的《中國土壤元素背景值》(國家環境保護局和中國環境監測總站,1990)中全國各省份土壤微量金屬元素背景值.
3.2.2 正態模糊數模型
模糊數法是針對區域土壤重金屬污染的模糊、不確定性特征所進行的評價,能更為全面地反映重金屬污染程度信息,可解決傳統的指數法評價難以描述土壤重金屬污染的不確定性問題.模糊數模型的核心是構建隸屬度函數,目前主要是采用線性形式來進行描述,例如三角與梯形模糊數法,本文采用正態模糊數評價方法,通過概率密度曲線間接反映隸屬度大小(易昊旻等,2013).
設論域為R+(正實數域)上的一個模糊數,定義A~的隸屬函數為:μ A(x):R→$0,1],x∈R,正態模糊數隸屬函數μA(x)表示為:
式中,μ為實測數據的平均值,σ為實測數據的標準差.A~作為一個模糊數僅具有概念上的意義,無法直接參與運算.實際應用時,一般通過α—截集將模糊數轉化為一定置信度水平的區間數.α—截集定義如下:
~∈F(U),對于任意α∈0,],記:(A~)αΔ AαΔ {μ|(μ)≥a}
一般而言,α取0.9是普遍可以接受的置信度水平(李如忠,2011),根據式(2)易求得區間數Aα:
然后計算一定置信度水平下區域重金屬的地累積指數區間數,對地累積指數區間數進行各污染等級的隸屬度計算,根據區間數對各污染程度等級的隸屬度,進行加權求和得出該區間數的重金屬污染程度.對于既得的正態隸屬度曲線,通過求取定積分的方式來獲取研究區土壤重金屬不同污染等級的面積占比.
3.2.3 核密度估計模型
核密度估計作為非參數估計理論中的一個典型方法,該方法的特點在于對采樣點數據的分布形式不作任何假定,僅依賴于數據本身,是完全數據驅動下的密度函數的估計.因此在土壤重金屬數據的信息挖掘上有很強的適用性.
對于樣本數據x1,x2...xn,核密度估計公式為:
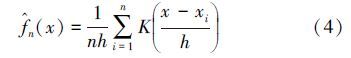
式中,K稱為核函數,n是總體樣本數,h為窗寬值或光滑系數.
核函數為關于y軸對稱并且其積分為1的概率密度函數,常用的核函數種類見表 1.根據以往學者的研究,不同核函數對結果的影響較小(郭照莊等,2008),本文選擇應用較為廣泛的高斯核函數進行研究.
表1 常見核函數類型
窗寬對核密度估計的結果十分重要,它的值如果過大,則核密度曲線會過于平滑,反之,則曲線會出現很嚴重的鋸齒.確定一個合理的窗寬值至關重要,最準確和科學的方法是計算核估計式關于真實概率密度函數的均方誤差(MSE),但這種方法卻不能在實際研究中進行應用,因為其用到了先驗知識.以本文的研究為例,若研究區重金屬含量的概率密度分布真實值已經掌握,就完全沒有進行核估計的必要,因此,該方法僅僅具有理論上的意義.
在不需要先驗知識的情況下,交叉驗證法對樣本數在100~1000的范圍內窗寬的選取精度較高(任溫軍和宋向東,2009),但容易陷入局部最優化.為了避免這種影響,本文將交叉驗證法所得窗寬值與實際應用中的一個經驗值取平均,作為最終的窗寬值.公式(5)為交叉驗證法選取窗寬的公式(吳喜之和趙博娟,2009):公式(6)為實際應用中確定窗寬的經驗公式,公式(7)為最終的窗寬公式.
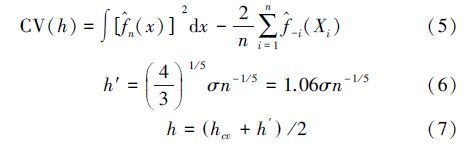
式中,f^-i(Xi)為刪去第i個觀測點之后得到的核密度估計.最優窗寬值hcv等價于使函數值CV(h)最小.對于重金屬的核密度曲線,區域總體污染程度以及各個污染等級面積的比重,也運用定積分來求取.
4 結果與討論
4.1 研究區土壤重金屬污染程度參照值的模擬
本文將采樣點數據進行克里格插值后所得到的柵格數據作為參照值,雖然該參照值本質上仍舊是離散的點,其統計結果與真實值相比仍存在誤差,但可以參照該值來測算各評價方法結果的偏差.
對柵格圖進行數據統計分析,可以得到表 2的數據作為評價的參照值.從表 2可以看出,參與統計的柵格圖像元值達到了50741個,數據量擴大了218倍.統計分析可知,研究區As、Cd的平均地累積指數參照值分別為-0.56、0.26,總體污染程度分別是清潔和輕度污染.
表2 研究區土壤重金屬地累積指數參照值
4.2 基于地累積指數的區域土壤重金屬污染程度評價
采用地累積指數法,通過取平均值計算區域總體污染程度,再按照各個樣點的污染程度等級進行簡單統計,得到各級別污染區域的面積占比.具體評價結果見表 3.從表 3結果可以看出,運用單純地累積指數進行評價偏差會較大,區域平均地累積指數相對于參照值的偏差分別為14.3%、19.2%.As在整個研究區的平均污染程度較低,總體污染程度評價結果偏低,各污染等級面積占比的偏差不大;各污染區域面積占比的偏差在Cd中體現較為明顯,重金屬污染評價結果偏高.總體上來看,運用簡單統計所得到的結果偏差比較大,如何在評價模型上進行一些改進以減少這種偏差很有必要.
表3 基于簡單地累積統計法的研究區土壤As、Cd污染程度評價結果
4.3 基于模糊數法的區域土壤重金屬污染程度評價 4.3.1 評價的過程與結果
研究區重金屬的正態或對數正態分布特征是運用正態模糊數法評價的前提條件和基礎,進行K-S檢驗,得到Cd的sig值為0.062,通過對As進行兩次對數轉換,其sig值為0.107,Cd、As在0.05的顯著水平下分別服從正態、對數正態分布,即可對研究區進行基于正態模糊數模型的As、Cd污染評價.
表4 基于正態模糊數的研究區土壤As、Cd污染程度評價結果
Cd計算得到標準化后清潔、輕度和中度污染面積占比分別是23.02%、71.96%、5.02%,偏差為+5.10%、-4.20%、-0.90%.與參照值相比,清潔區域面積占比有所提高,而輕度和中度污染的區域面積占比有不同幅度的下降,總體評價結果有一定程度偏低.As計算結果為歸一化后清潔、輕度和中度污染面積占比分別為99.81%、0.19%、0,清潔、清度污染的偏差分別為+0.11%、-0.11%.結合表 3的結果,該占比結果更加接近于參照值,說明對于占比十分微小的輕度污染面積占比,正態模糊數模型仍有一定的識別功能.
4.3.2 與傳統的線性模型評價結果的定量比較
基于模糊數模型的土壤重金屬污染程度評價,更多學者選擇的是線性模糊數,其中的典型代表是三角模糊數,本文運用三角模糊數進行研究區污染程度評價,并將其評價結果與正態模糊數的結果進行定量比較.三角模糊數的原理、公式可參見相關文獻(李飛等,2012),截集α仍選擇0.9,計算結果見表 5.
表5 基于三角模糊數的研究區土壤As、Cd污染程度評價結果
從表 5可以看出,與正態型模糊數相比,三角模糊數的模糊地累積指數區間發生了正向偏移,使得評價地累積指數大于正態模型.結合參照值可知,這種正向偏移使As的偏差減小到10.54%,但使Cd的偏差大幅增加到52.42%,顯示出線性模糊數的評價結果具有較強的波動性.同時,從各等級污染區域占比看出,三角模糊數會使區間值范圍有所縮小.與參照值的各等級污染面積占比相比,As的輕度污染區域占比減小,而清潔區域占比增大;Cd的清潔區域和中度污染區域占比進一步減小,而輕度污染區域占比增大,從而使其污染比重有所提高.因此,三角模糊數的評價結果較差.
4.4 基于核密度估計法的區域土壤重金屬污染程度評價
對核估計式繪圖得到As、Cd含量的概率密度曲線(圖 2),從曲線形狀可知,As含量的概率密度確實呈現一定程度的正偏態,概率最高值出現在7.2 mg · kg-1,在其右側的最大值達到了12 mg · kg-1左右,而左側在5.5 mg · kg-1之下就出現幾率基本為0.計算后得到研究區As地累積指數平均值為-0.62,地累積指數的方差為0.24,說明核密度估計法能對區域As總體污染程度的準確度評估方面有一定提高,并且運用核密度估計后的數據的標準差也與參照值一致,反映了評估結果較為穩定可靠.接下來再根據核密度估計曲線對As各個污染程度的面積比重進行計算.計算結果為:清潔區域污染比重為99.87%,輕度污染區域的比重是0.13%.各級污染區域比重與模糊數法相比類似,而核估計法輕度污染區域的評估比重稍低,但也能較敏感的顯示占比很小的輕度污染區域.
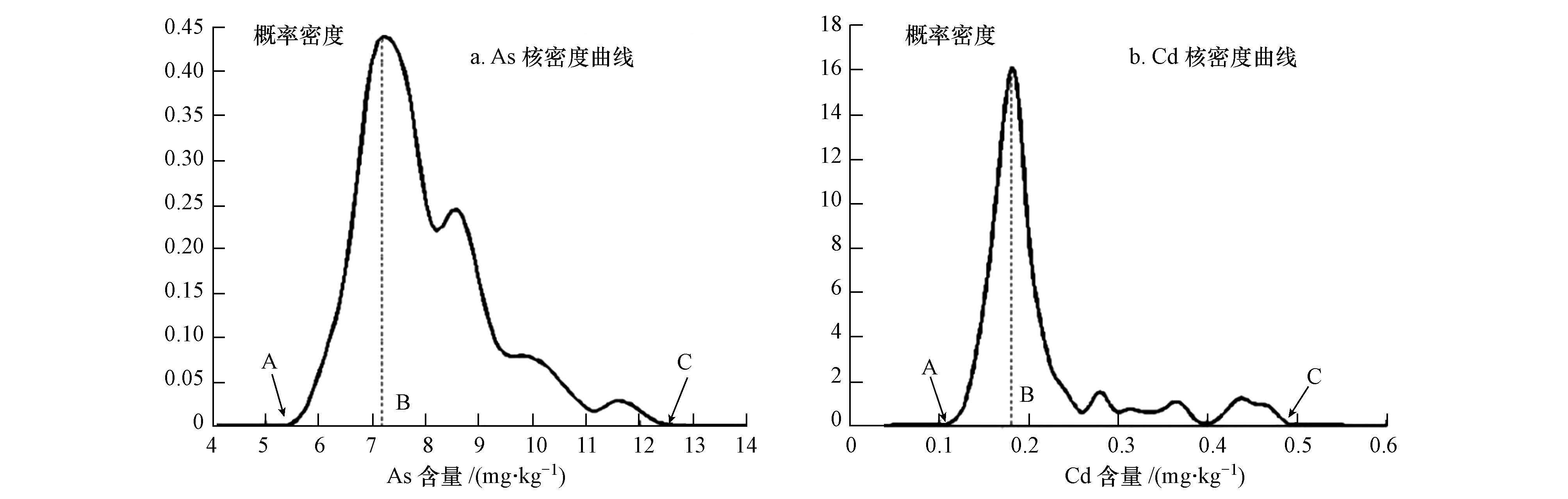
圖2 As、Cd含量核密度估計曲線
Cd也存在一定程度的正偏態,含量值絕大部分分布在0.1~0.25 mg · kg-1,其中概率密度最高的值在1.8 mg · kg-1左右.相較于As,Cd元素的曲線峰度也很大,含量值在0.01 mg · kg-1之前出現頻率基本為0,從0.1~0.2迅速上升至最高點,再從0.2~0.26驟降至很低的概率密度值,這和As元素的階梯式下降有所不同.0.3~0.5 mg · kg-1高含量值區間有嚴重拖尾現象,該區間概率密度值均很低,這有可能是部分區域的人為污染造成.對Cd的總體污染水平進行計算,得到研究區Cd地累積指數平均值為0.30,地累積指數的方差為0.36.最后對各個污染級別的面積占比進行統計,清潔區域占比18.40%,輕度污染區域占比為70.96%,中度污染區域占比10.64%.與參照值相比,輕度與中度污染區域面積有5%左右的偏差,這可以解釋為核估計模型對稀少值的一種敏感性,即Cd曲線中區間$0.3~0.5]的點位稀少,通過評估,每個點位的出現都會使其附近值的出現幾率增加,反映在概率密度曲線上,就是連續不間斷的拖尾現象.
4.5 不同評價方法下區域土壤重金屬污染程度的綜合比較
本文采用不同方法對研究區As、Cd兩種土壤重金屬元素的污染程度進行了污染評價.以地累積指數為污染指數,分別采用了簡單數理統計、模糊數法以及核密度估計方法進行了評價.3種方法從評價便捷性上是由易到難的,但運用更為復雜的模型會提高評價結果的準確度或全面性.相關評價結果見圖 3.
圖3(Fig.3)
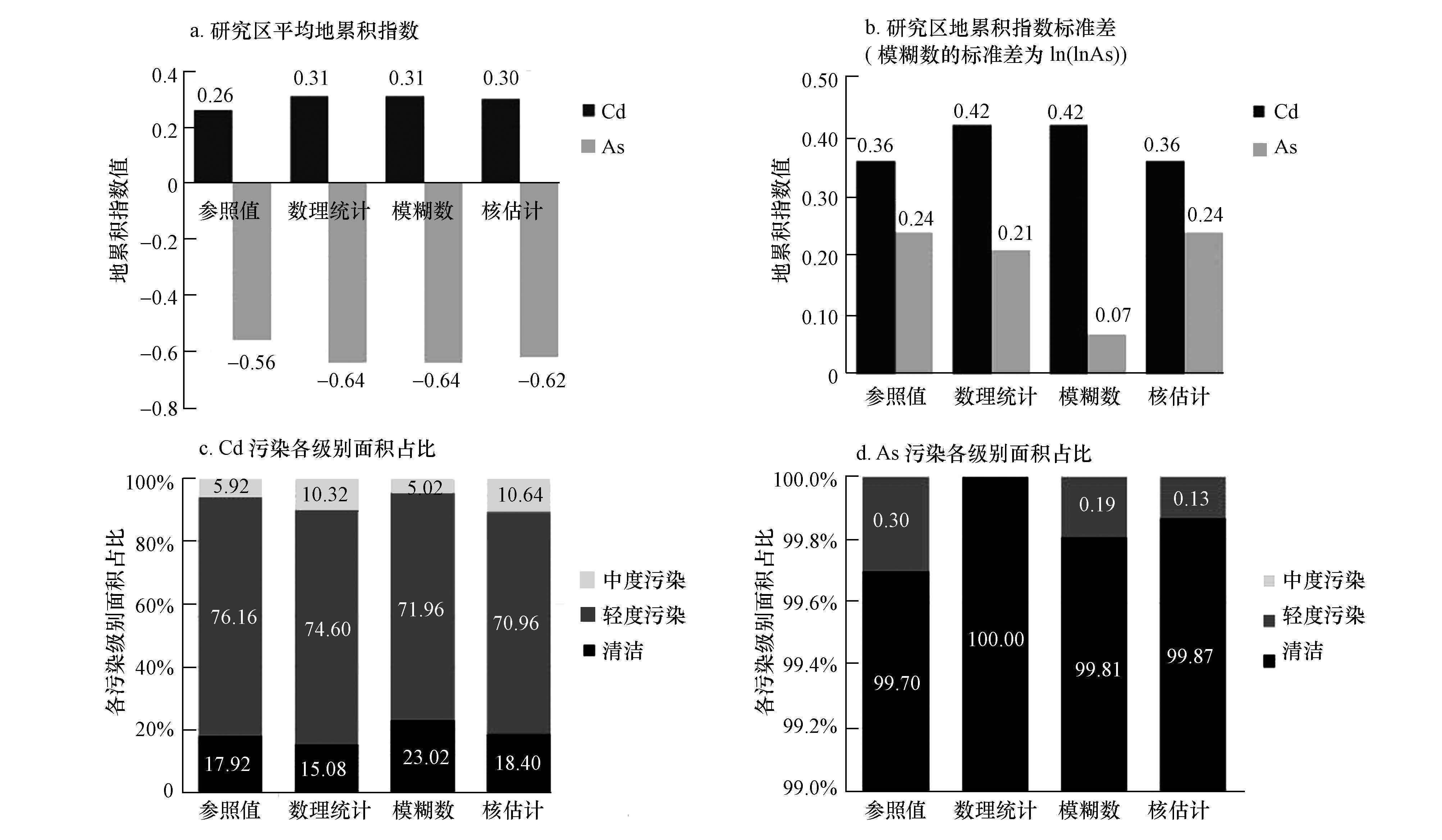
圖3 As、Cd不同評價方法結果的綜合比較
從簡單數理統計上來說,評估的結果較為良好,準確度和參照值相差不大,但是對各污染等級面積占比的測度不夠準確,會遺漏研究區域分布極少的污染等級面積占比,這種情況在對As元素各污染級別的面積比重測算中有所體現,即遺漏了面積占比極少量的輕度污染區域.而運用模糊數與核估計模型進行評估就能在一定程度上避免了這個問題.
模糊數模型與簡單數理統計的結果一致,原因在于模型的兩個重要參數——均值與標準差就是基于樣本數據,故不能提高對總體污染程度評估的準確度.但運用正態模糊數法仍然有兩個優點:①通過隸屬度曲線能對各污染等級面積占比有比較準確的測度,能較為敏感地統計出研究區域分布極少的污染等級面積占比;②也能在一定置信水平下用一個區間數來表征區域土壤重金屬總體污染程度,能更為全面地反映區域土壤重金屬污染程度,評價結果所涵蓋的信息更加全面.
核密度估計則突破了模糊數對分布條件的限制,對任何分布形式的數據均能統計出所有可能值的概率密度,并通過一定的公式轉化求得該重金屬的區域總體污染程度以及各污染級別面積占比.從圖 3的結果可知,評價結果的準確度能在前兩種方法基礎上有一定提高,且從標準差上可以看出,很好的保持了樣本數據的穩定性,因此,核估計的評價結果能更準確地反映研究區土壤重金屬污染實際,但它有兩個缺點:一是計算量比較大,手動計算起來很繁瑣,通常需要通過程序來支持運算,可考慮借助軟件編程來實現;二是窗寬值的大小對核估計的效果起著決定性作用,但是窗寬的合理估計值往往是較難確定的.核密度估計方法的模型架構較為靈活多變,同時由于估計式可以依賴代碼程序實現,允許它的估計過程更為復雜,故有著很大的改造空間.比如王金然等(2005)運用迭代算法對核函數模型進行優化,通過對核密度函數進行迭代,進一步提高區域土壤重金屬污染程度評價的準確度,鑒于其運算量在核密度估計的基礎上又有了數量級的增加,在較多指標與樣本數的情況下評價效率會比較低,如何在保證準確度的同時,提高核估計迭代式的評價效率是值得進一步研究的問題.具體參見污水寶商城資料或http://www.bnynw.com更多相關技術文檔。
5 結論
區域土壤重金屬污染不同評價方法的結果有所不同,各方法在評價便捷性、結果的準確度和包含信息的全面性方面也有所差異:
1)簡單數理統計評價便捷性最高,但結果準確度較低,對各污染等級面積占比的測度不夠準確,會遺漏研究區內分布極少的污染等級面積占比,并且只能得出唯一值,結果所包含信息較少.
2)應用正態模糊數法評價能通過隸屬度曲線能對各污染等級面積占比有比較準確的測度,此外也能在一定置信水平下用一個區間數來表征區域土壤重金屬總體污染程度,評價結果所涵蓋的信息更加全面,結果所包含信息最多,但基于正態模糊數法與簡單數理統計的總體污染程度評價結果偏差一致,結果準確度較低,并且正態模糊數法采用較為復雜的數學模型,評價便捷性遠低于簡單數理統計.與正態模糊數法相比,三角模糊數法評價結果具有較強的波動性,評價結果較差.
3)核密度估計結果準確度最高,該方法下研究區As和Cd總體污染評價的平均地累積指數相對于參照值的偏差僅分別為10.7%和15.4%,但是核密度估計模型計算最為復雜,需要通過程序來支持運算,評價便捷性最差,并且只能得出唯一值,結果所包含信息較少.同時對核密度估計效果起著決定性作用的窗寬合理估計值往往是較難確定的,但由于其靈活多變模型架構和計算可以依賴代碼程序實現的特點,核密度方法有著很大的改造空間.







